A particle (a mud pallet, say) of mass m strikes a smooth stationary wedge of mass M with as velocity v0 at an angle θ with horizontal. If the collision is perfectly inelastic, find the
a. velocity of the wedge just after the collision.
b. Chane in KE of the system (M+m) in collision.
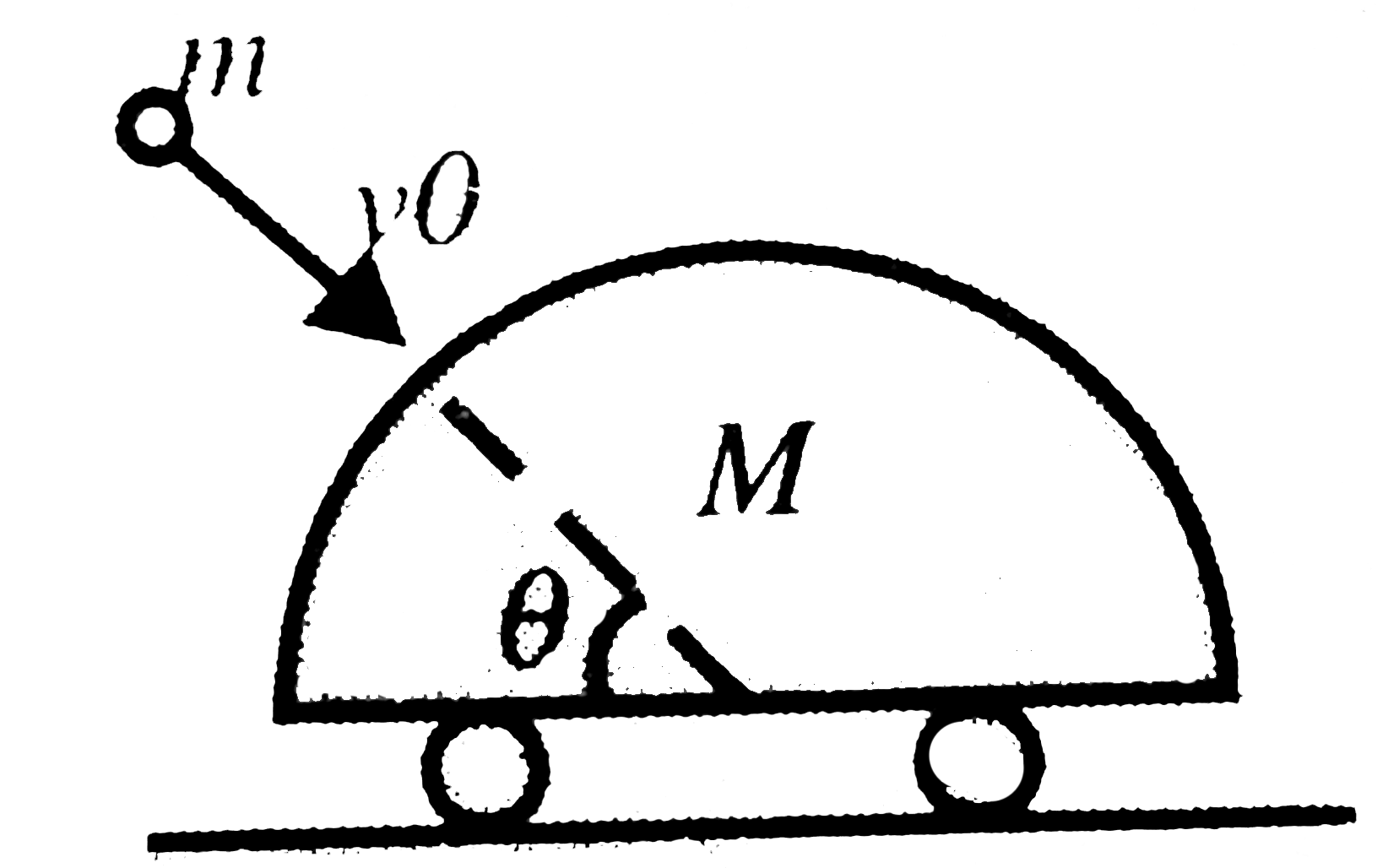
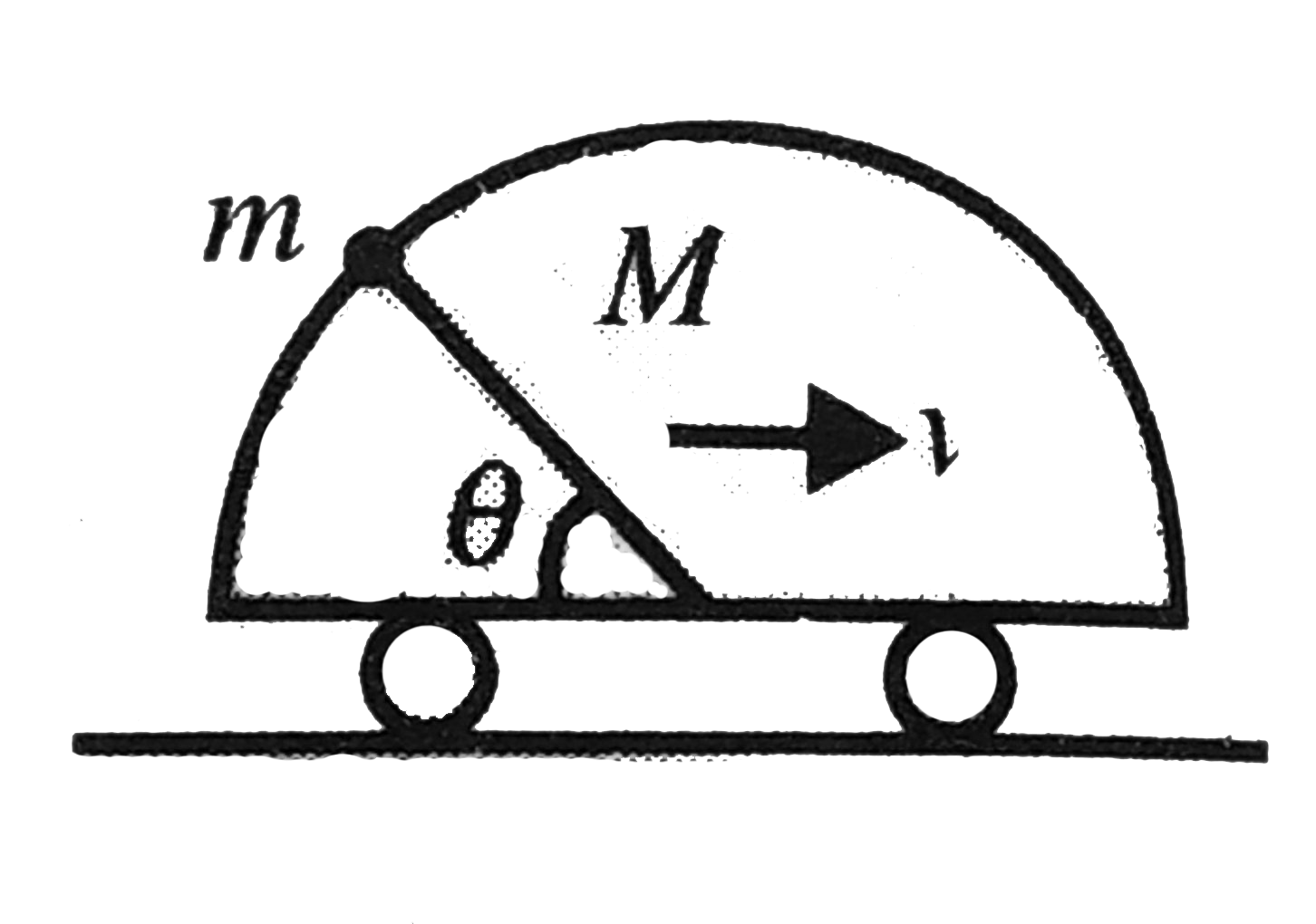
a. Let the system (M+m) moves as a single mass with a velocity v.
conserving the momentum of the system in horizontal, we have
mv0cosθ=(M+m)v
This gives v=mv0cosθM+m
b. the change in KE of the system is
△K=12(M+m)v2−12mv20
where v=mv0cosθM+m ltbr This gives △K=(M+m)2(mv0cosθ(M+m)2−12mv20
=−mv202(1−mM+mcos2θ)
=−(M+msin2θ)mv202(M+m)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples13videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
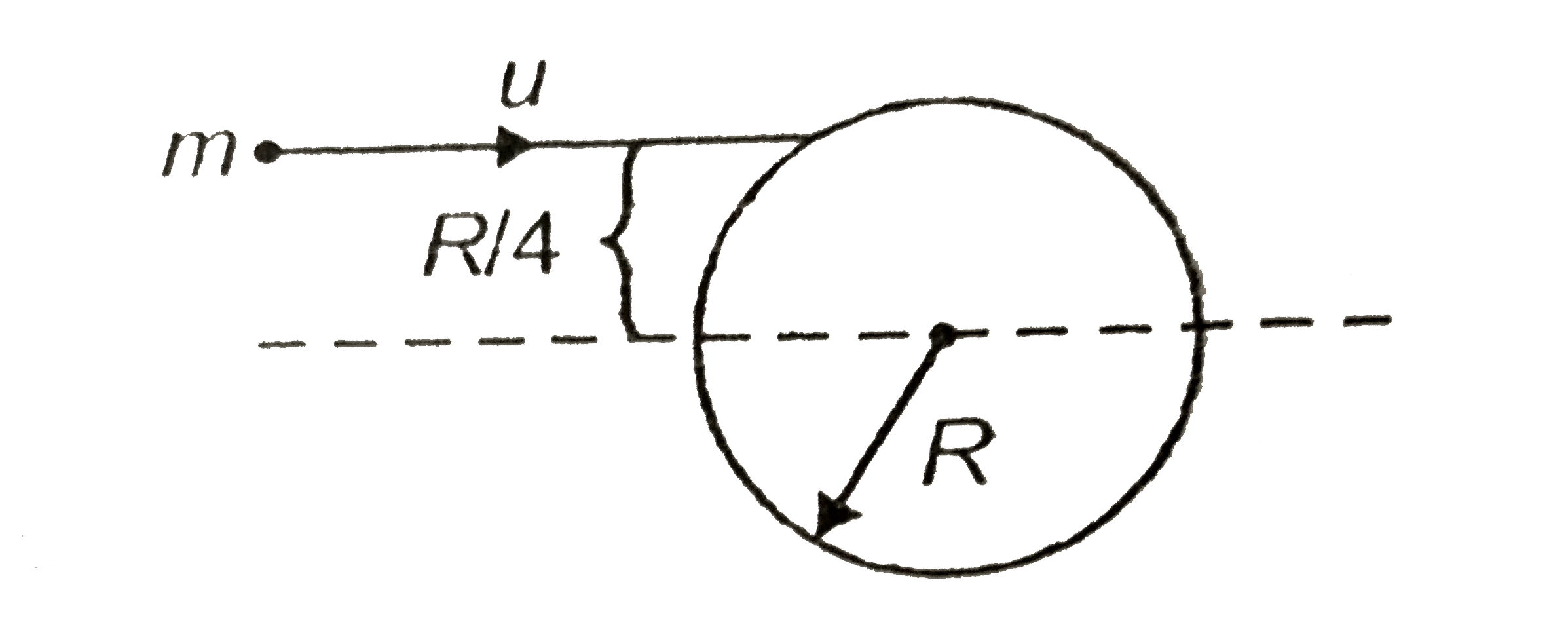 View Solution
View SolutionA particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
Aπ4Bπ3Cπ6Dπ2 - Question 2 - Select One
A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
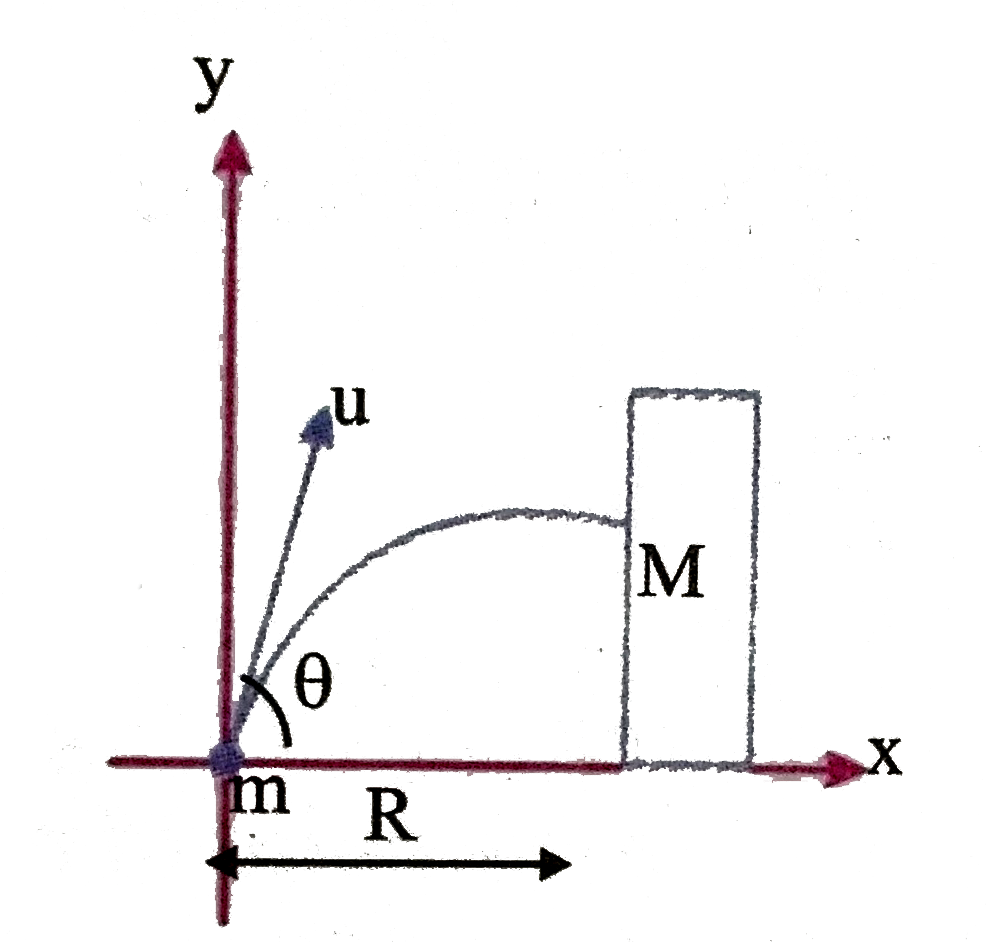
FInd the velocity of the ball after collisionA(m−eMM+m)ucosθB(M−emM+m)ucosθC(m+eMM+m)usinθD(m−eMM+m)usinθ - Question 3 - Select One
Two balls of masses m each are moving at right angle to each other with velocities 6 m/s and 8 m/s respectively. If collision between them is perfectly inelastic, the velocity of combined mass is
A15 m/sB10m/sC5 m/sD2.5 m/s
A tiny ball of mass m is released from the state of rest over a large smooth sphere of mass M and radius R, which is at rest on a smooth horizontal surface. If the ball strikes the sphere perfectly inelastically, find their velocities after collision.
 View Solution
View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.
 View Solution
View SolutionA particle of mass m moving on a smooth surface with velocity 10m/s strikes another particle of mass 2m moving with 5m/s in the same direction . If the collision is elastic and head - on , find velocities of particles after the collision.
View SolutionTwo particles of masses 0.5 kg and 0.25kg moving with velocity 4.0 m/s and -3.0m/ collide head on in a perfectly inelastic collision. Find the velocity of the composite particle after collision and KE lost in the collision.
View SolutionA particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
View Solution

