A particle having a charge of 2.0X10−8C and a mass of 2.0X10−10g is projected with a speed of 2.0X103ms−1 in a region having a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
To solve the problem step by step, we will first identify the given values, then calculate the radius of the circular path of the charged particle in the magnetic field, and finally calculate the time period of the motion.
Step 1: Identify the Given Values
- Charge of the particle, Q=2.0×10−8C
- Mass of the particle, m=2.0×10−10g=2.0×10−10×10−3kg=2.0×10−13kg
- Speed of the particle, v=2.0×103m/s
- Magnetic field strength, B=0.10T
Step 2: Calculate the Radius of the Circular Path
The formula for the radius r of the circular path of a charged particle moving in a magnetic field is given by:
r=mvQB
Substituting the values into the formula:
r=(2.0×10−13kg)(2.0×103m/s)(2.0×10−8C)(0.10T)
Calculating the numerator:
2.0×10−13×2.0×103=4.0×10−10kg m/s
Calculating the denominator:
(2.0×10−8C)(0.10T)=2.0×10−9C T
Now, substituting these into the radius formula:
r=4.0×10−102.0×10−9=0.2m
Thus, the radius of the circular path is:
r=0.2m=20cm
Step 3: Calculate the Time Period of the Motion
The formula for the time period T of the circular motion is given by:
T=2πrv
Substituting the values:
T=2π(0.2m)2.0×103m/s
Calculating 2π:
2π≈6.28
Now substituting:
T=6.28×0.22.0×103=1.2562000=6.28×10−4s
Thus, the time period of the motion is:
T=6.28×10−4s
Final Answers
- Radius of the circular path: r=0.2m or 20cm
- Time period of the motion: T=6.28×10−4s
- Charge of the particle, Q=2.0×10−8C
- Mass of the particle, m=2.0×10−10g=2.0×10−10×10−3kg=2.0×10−13kg
- Speed of the particle, v=2.0×103m/s
- Magnetic field strength, B=0.10T
The formula for the radius r of the circular path of a charged particle moving in a magnetic field is given by:
The formula for the time period T of the circular motion is given by:
- Radius of the circular path: r=0.2m or 20cm
- Time period of the motion: T=6.28×10−4s
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
A particle having a charge of 5.0μC and a mass of 5.0X10−12kg is projected with a speed of 1.0kms−1 in a magnetic field of a magnetic field of magnitude 5.0 m T. The angle between the magnetic field and the velocity is sin−1(0.90). show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.
View SolutionA particle having a charge of 100μC and a mass of 10mg is projected in a uniform magnetic field of 25m T with a speed of 10ms−1. If the velocity is perpendicular to the magnetic field , how long will it take for the particle to come back to its original position for the first time after being projected.
View SolutionA proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionAn α - particle with a specific charge of 2.5×107Ckg−1 moves with a speed of 2×105ms−1 in a perpendicular magnetic field of 0.05T. Then , the radius of the circular path described by it is
View SolutionFind the centre and the radius of the circle x2+y2+8x+10y−8=0.
View SolutionA particle of mass m=1.6X10−27 kg and charge q=1.6X10−19 C moves at a speed of 1.0X107ms−7. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at E.
 View Solution
View SolutionA proton is projected with a speed of 3X106ms−1 horizontally from est to west. A uniform magnetic field →Bofstren>h2.0X10−3 T exists in the vertically upward direction(a) find the force on the proton just after it is projected. (b) what is the acceleration produced?
View SolutionA proton is projected with a speed of 3X106ms−1 horizontally from east to west. A uniform magnetic field →B of strength 2.0X10−3 T exists in the vertically upward direction(a) find the force on the proton just after it is projected. (b) what is the acceleration produced?
View SolutionFigure shows a convex lens of focal length 10cm lying in a uniform magnetic field B of magnitude 1.2T parallel to its principal axis.A particle havig a charge 2.0×10−3C and mass 2.0×10−5kg is projected perpendicular to the plane of the diagram with a speed of 4.8m/s.The particle moves along a circle with its centre on the principal axis at a distance of 15cm from the lens.The axis of the lens and of the circle are same.Show that the image of the particle goes along a circle and find the radius of that circle.
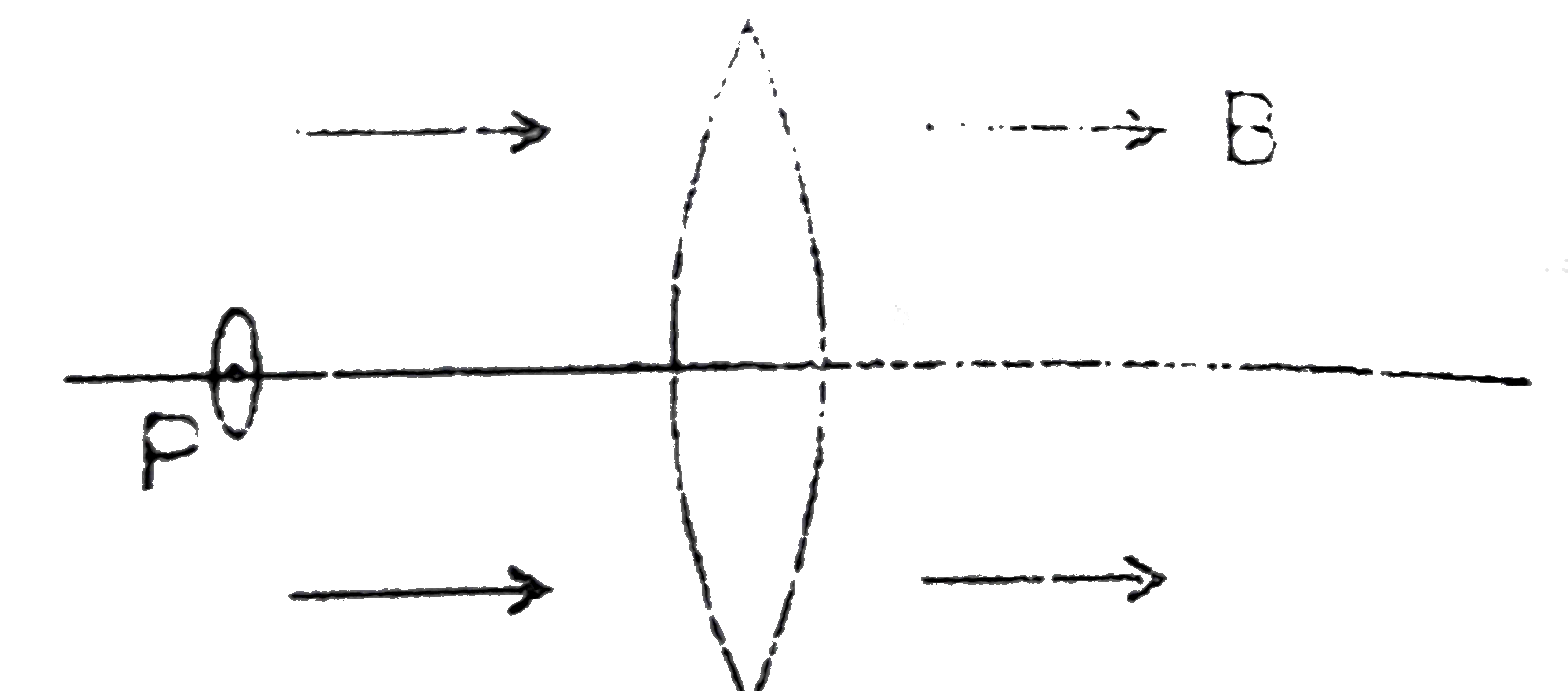 View Solution
View Solution

