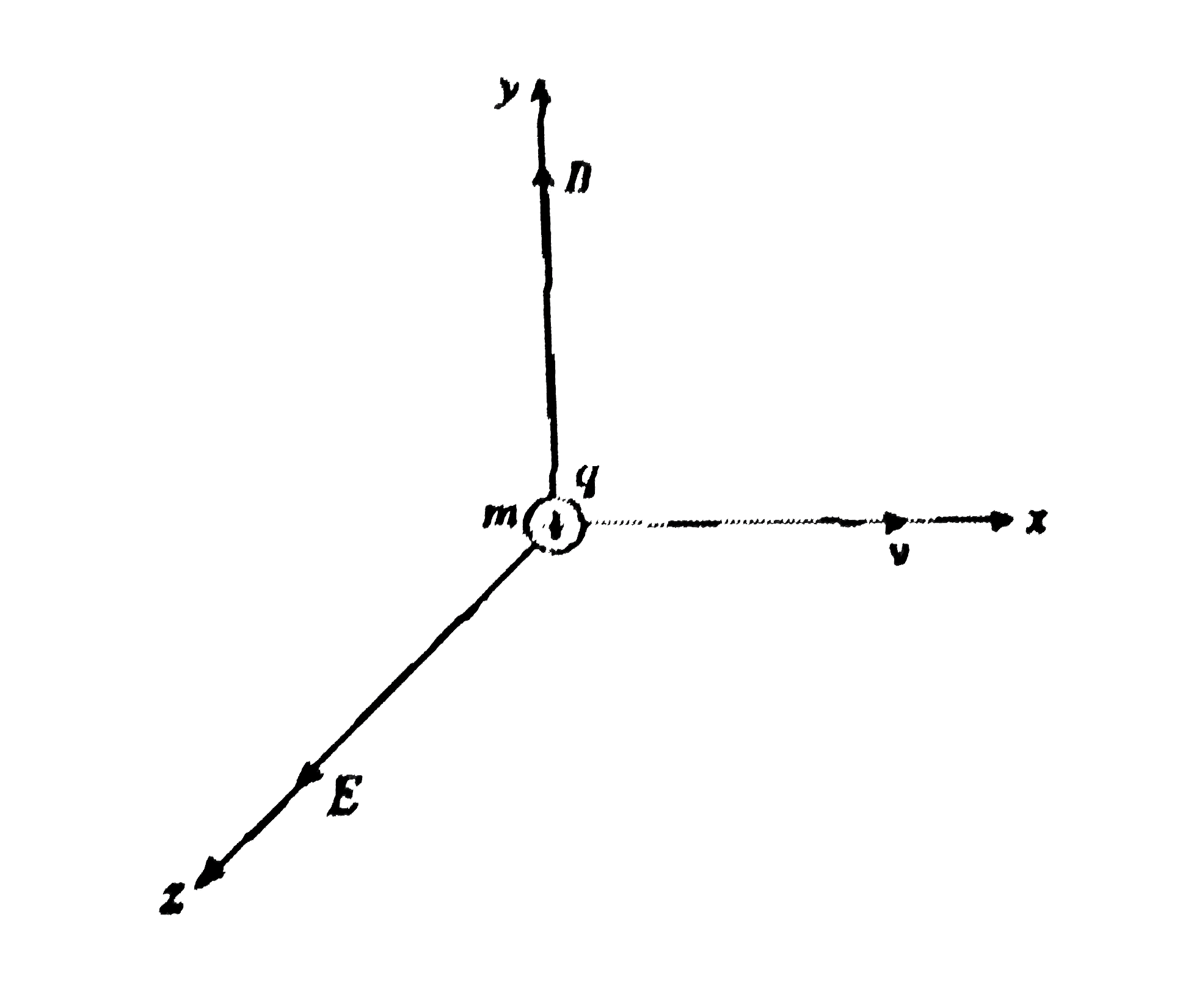
A particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0ˆjand→E≡E0ˆk.
Find the speed of the particle as a function of its z-coordinate.Solution in Gujrati
Velocity will be along x−zpla≠−¯¯¯B
=−¯¯¯B0¯¯¯J,¯¯¯E=E0¯¯¯¯K
F=q(E+V×B)
=qE0K−qVxB0K+qVxB0I
SinceVx=0,F2=qE0
so a=qE0m
∴V2=u2+2as=2qE0□mz
so,v=√2qE0zm
[dist along z - direction be z ].
Topper's Solved these Questions
Similar Questions
If a charged particle at rest experiences no electromagnetic force, then electric field in that region
05:16View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
03:46View SolutionUsing the formulae ((→F)=(→qv)×(→B)and(B=(μ0)i2πr), show that the SI units of the magnetic field B and the permeability constant (μ0) may be written as (NmA−1) and (NA−2) respectively.
07:37View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E=E0→K.
Find the speed of the particle as a function of its z-coordinate.05:56View SolutionA particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.04:28View SolutionA particle is released from the origin with a velocity vˆe(i). The electric field in the region is Eˆe(i) and magnetic field is Bˆk. Then
02:22View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and megnetic field are given by →B=−B0ˆj and →E=→E0ˆk. Find the speed of the particle as a function of its z-coordinate.
14:57View SolutionA particle of mass m and charge q is thrown from origin at t=0 with velocity 2hati+3hatj+4hatk units in a region with uniform magnetic field vecB=2hati units. After time t=pim//qB , an electric field vecE is switched on such that particle moves on a straight line with constnat speed vecE may be:
04:23View SolutionA charge particle of charge q, mass m is projected with a velocity →v=vˆi in a region of space where electric field strength →E=Eˆk and magnetic induction →B=Bˆj are present. The acceleration of the particle is:
 03:17View Solution
03:17View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are ginen by B=+B_(0)hatj and vecE=+E_(0)hati . Find the speed of the particle as a function of its X -coordinate.
03:15View SolutionElectric field strength vecE = E_0 hati and vecB = B_0 hati exists in a region. A charge is projected with a velocity vecv = v_0 hatj origin, then
01:53View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E−E0→K.
Find the speed of the particle as a function of its z-coordinate.01:46View SolutionA particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of is
02:51View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
05:15View SolutionElectric field and magnetic field in a region of space are given by(Ē= E_0 hat j). and (¯¯¯B=B0ˆj). A charge particle is released at origin with velocity (¯v=v0ˆk) then path of particle is
05:24View SolutionA particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.02:15View Solution

