A particle is moving along a vertical circle of radius R=20m with a constant speed v=31.4m/s as shown in the figure. Straight line ABC is horizontal and passes through the centre of the circle. A shell is fired from point A at the instant when particle is at C. The distance AB is 20√3m and shell collides with the particle at B, if smallest possible value of the angle of projection is k×10∘ then find the value of k.

As at the time of firing of th shell , the particle was at C and the shell collides with it at B, therefore the number of the revolution completed by the particle is odd multiple of half i.e., (2n-1)/2, where n is an integer .
Let the time period of the particle , then
T=2πrv=2×3014×2031.4=4 second.
IF the time of the flight of the shell , then t = time of [(2n−1)/2] revolutions of the particle
=(2−1)2×4=2(2n−1) second .
for a projectile , the time of flight is given by t=2usinθg
Hence 2usinθg=2(2n−1) .......(i)
The range of the projectile is given by R=u2sin2θg
Hence u2sin2θg=20√3 ........(ii)
From equation (i) and (ii) tanθ=(2n−1)2√3
For θ to be smallest , n =1 so tanθ=(2n−1)√3
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
A particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
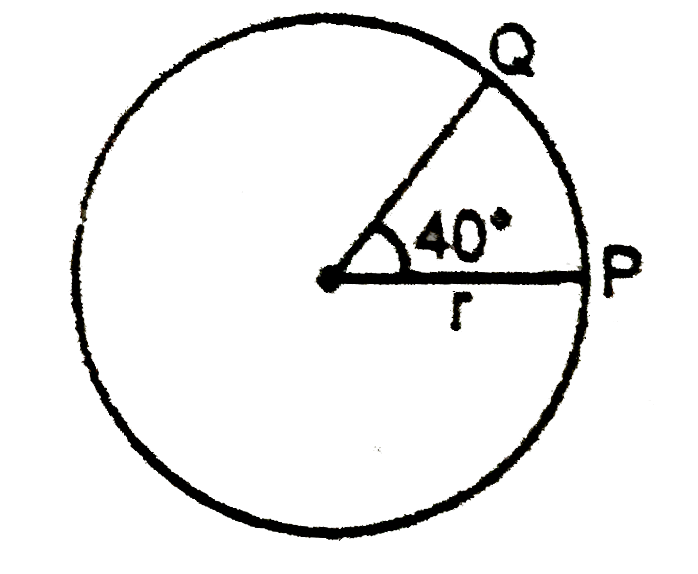
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
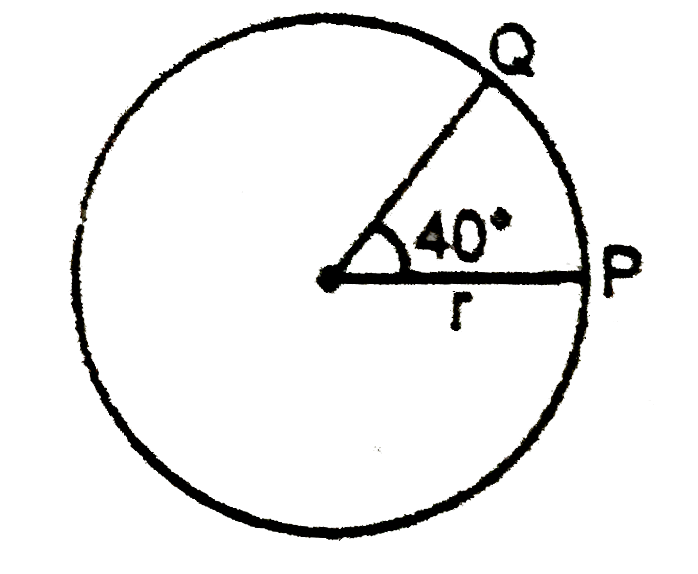
View SolutionA particle is moving in a circle of radius r having centre at O with a constant speed v . The magnitude of change in velocity in moving from A to B is
View Solution
Particle P shown in figure is moving in a circle of radius R=10 cm with linear speed v=2m/s Find the angular speed of particle about point O.
View SolutionA particle P is moving in a circle of radius 'a' with a uniform speed v. C is the centre of the circle and AB is a diameter. When passing through B the angular velocity of P about A and C are in the ratio
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View Solution
