A particle is moving in a straight line and relationn between time and displacement is t=ax2+βx. If retardation is found to be proportional to the vn, where v is instantaneous velocity, find the value of n.
The correct Answer is:3
To solve the problem, we need to analyze the given relationship between time (t) and displacement (x) and find the value of n, where retardation is proportional to vn.
1. Given Relation:
The relation between time and displacement is given as:
t=ax2+βx
2. Differentiate to Find Velocity:
We differentiate t with respect to x to find dtdx:
dtdx=ddx(ax2+βx)=2ax+β
Now, to find velocity v, we take the reciprocal:
v=dxdt=1dtdx=12ax+β
3. Differentiate to Find Acceleration:
Acceleration a is defined as dvdt. We need to differentiate v with respect to t:
a=dvdt=ddt(12ax+β)
Using the chain rule:
a=−1(2ax+β)2⋅d(2ax+β)dt
Now, we need to find d(2ax+β)dt:
d(2ax+β)dt=2adxdt=2av
Therefore, substituting back:
a=−2av(2ax+β)2
4. Express Acceleration in Terms of Velocity:
We can express a in terms of v:
a=−2av(2ax+β)2
Notice that (2ax+β) can be replaced with 1v:
a=−2av(1v)2=−2av3
5. Relate Acceleration to Retardation:
Since retardation is negative acceleration, we can write:
|a|=2av3
This implies that retardation is proportional to v3:
|a|∝v3
6. Conclusion:
From the above derivation, we conclude that the value of n is:
n=3
Final Answer:
The value of n is 3.
The relation between time and displacement is given as:
t=ax2+βx
We differentiate t with respect to x to find dtdx:
dtdx=ddx(ax2+βx)=2ax+β
Now, to find velocity v, we take the reciprocal:
v=dxdt=1dtdx=12ax+β
Acceleration a is defined as dvdt. We need to differentiate v with respect to t:
a=dvdt=ddt(12ax+β)
Using the chain rule:
a=−1(2ax+β)2⋅d(2ax+β)dt
Now, we need to find d(2ax+β)dt:
d(2ax+β)dt=2adxdt=2av
Therefore, substituting back:
a=−2av(2ax+β)2
We can express a in terms of v:
a=−2av(2ax+β)2
Notice that (2ax+β) can be replaced with 1v:
a=−2av(1v)2=−2av3
Since retardation is negative acceleration, we can write:
|a|=2av3
This implies that retardation is proportional to v3:
|a|∝v3
From the above derivation, we conclude that the value of n is:
n=3
The value of n is 3.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS )
1 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
A particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View Solution
Knowledge Check
A particle move in a straight line with retardation proportional to its displacement its loss of kinectic energy for any displacement x is proportional to
AxBe2Cx2DlogexA particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to
Ax2BexCxDlogexA particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to
Ax2BexCxDlogex
A particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
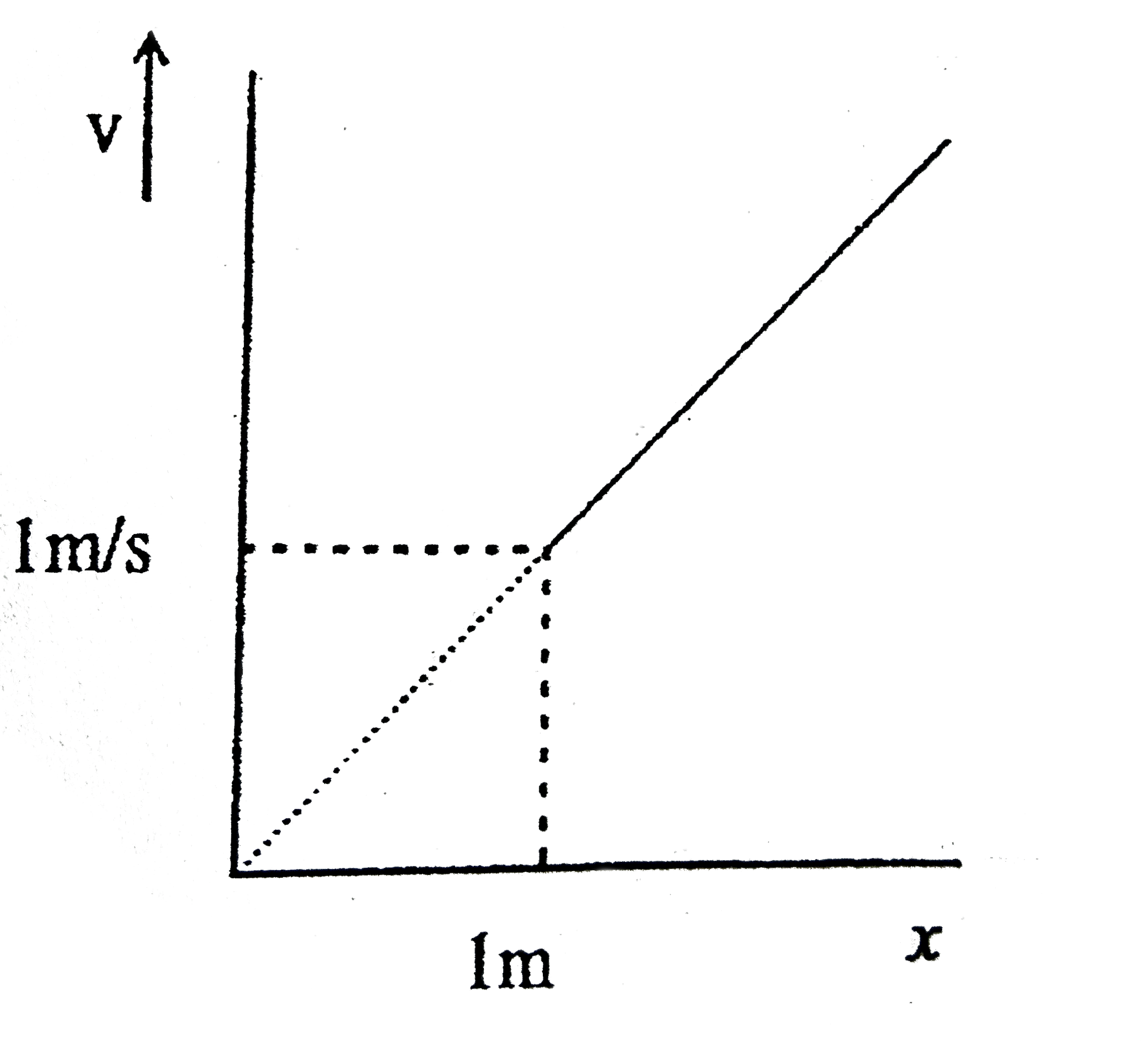
View SolutionA body at rest is moved in a stright line by supplying constant power to it . Distance moved by the body in time t is found to be proportional to tn Value of n is .
View SolutionFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
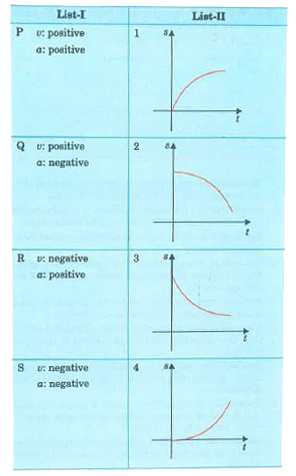
View SolutionA particle is moving in a straight line. Its displacement at time t is given by s(Inm)=4t2+2t, then its velocity and acceleration at time t=12 second are
View Solution
