A particle is performing SHM according to the equation x=(3cm)sin(2π18+π6), where t is in seconds. The distance travelled by the particle in 39 s is
24cm
1.5cm
25.5cm
none of these
The correct Answer is:C
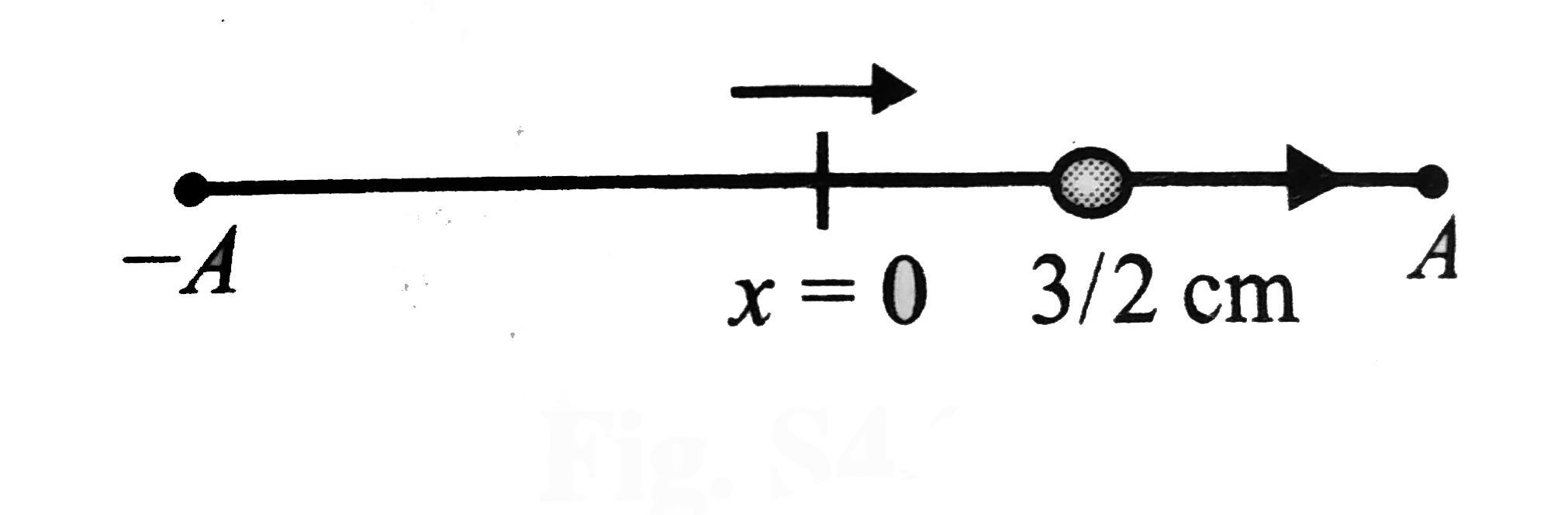
The time period of simple harmonic motion is T=18s.
At t=0 the particle is at x=32cm and approaching position extreme.
39s=2×18+3=2T+3=2T+T6
distance travelled by the particle is 2T is 8A=24cm.
distance travelled by the particle in further
T6 is A2=1.5cm.
Total distance travelled=25.5cm
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
x−t equation of a particle in SHM is
x=(4cm)cos(π2t)
Here ,t is in seconds. Find the distance travelled by the particle in first three seconds.
View SolutionA particle is moving along the x-axis such that s=6t−t2, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5s.
View Solution
Knowledge Check
A particles executes SHM according to the equation y = 2 sin 2πt, where y is displacement in m and t is time in s. The distance covered by the particle in 4 s of its motion is
A0B2 mC8 mD32 mA particle executes SHM according to equation x=10(cm)cos[2πt+π2], where t is in seconds. The magnitude of the velocity of the particle at t=16s will be :-
A24.7 cm/sB20.5 cm/sC28.3 cm/sD31.4 cm/sThe position of a particle is defined by →r=2sin(π4)tˆi+2cos(π4)tˆj+3tˆk , where 't' is in seconds. Then distance travelled by particle in 2 second motions is. [useπ2=10]
A√32mB√46mC√56mDNone of these
A particle executes simple harmonic motion according to the displacement equation y=10cos(2πt+π6)cm where t is in second The velocity of the particle at t=16 second will be
View SolutionA particle executing SHM according to the equation x=5cos(2πt+π4) in SI units. The displacement and acceleration of the particle at t=1.5 s is
View SolutionA particle is oscillating according to the equation x=8cosπt, where 't' is in second. The particle moves from the position of equilibrium to maximum displacement in time
View SolutionA particle osciallates with SHM according to the equation x=(2.5m)cos[(2πt)+π4] . Its speed at t=1.5 s is
View SolutionA particle oscillates with S.H.M. according to the equation x=10cos(2πt+π4). Its acceleration at t=1.5s is
View Solution
