A physical pendulum is positioned so that its centre of gravity is above the suspension point. When the pendulum is realsed it passes the point of stable equilibrium with an angular velocity ω. The period of small oscollations of the pendulum is
4πω
2πω
πω
π2ω
The correct Answer is:A
12Iω2=mg(2l)⇒Imgl=4ω2
T=2π√Imgl=2π√4ω2=4πω
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Two physical pendulums perform small oscillations about the same horizontal axis with frequencies ω1 and ω2 . Their moments of inertia relative to the given axis are equal to I1 and I2 respectively. In a state of stable equilibium the pendulums were fastened rigifly together. What will be the frequency of small oscillations of the compound pendulum ?
View SolutionStatement-1: The pendulum shown in the figure consists of a bob suspended by a light rigid rod. The pendulum is suspended from the ceilling of a heavy wooden box which hcan freely fall on the guiding wires. Initially the box is at rest and the pendulum is released from the position shown. When the pendulum becomes vertical the box starts falling freely. The pendulum will move with a constant angular speed w.r.t box
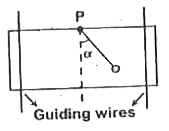
because
Statement-2: The angular acceleration of the pendulum w.r.t. P once the box starts falling freely is zero.
View Solution
Knowledge Check
A particle pendulum is positioned such that is centre of gravity is vertically above suspension point. From that position the pendulum started moving tward the stable equilibroum and passed it with an angular velocity ω. By neglecting the friction at point of suspension, the period of small oscillations of the pendulum is
A2πωB4πωCπωD5πωWhen the point of suspendion of pendulum is moved, its period of oscillation
Adecreaes when it moves vertically upwards with an acceleration aBdecreases when it moves vertcally downwards with acceleration greater than 2 g.CIncreases when it moves horizontally with acceleration aDall of the above.Two identical simple pendulums each of length 'l' are connected by a weightless spring as shown. In equilibrium, the pendulums are vertical and the spring is horizontal and undformed. The time period of small oscillations of the linked pendulums, when they are deflected form their equilibrium positive through equal displacements in the same vertical plane in the opposite directions and released, is
 A2π√lgB2π ⎷l(g+2klm)C2π ⎷l(g+klm)D2π√2lg+mk
A2π√lgB2π ⎷l(g+2klm)C2π ⎷l(g+klm)D2π√2lg+mk
A simple pendulum has time period T. Charges are now fixed at the point of suspension of the pendulum and on the bob. If the pendulum continues to oscillate, its time period will now be
View Solution
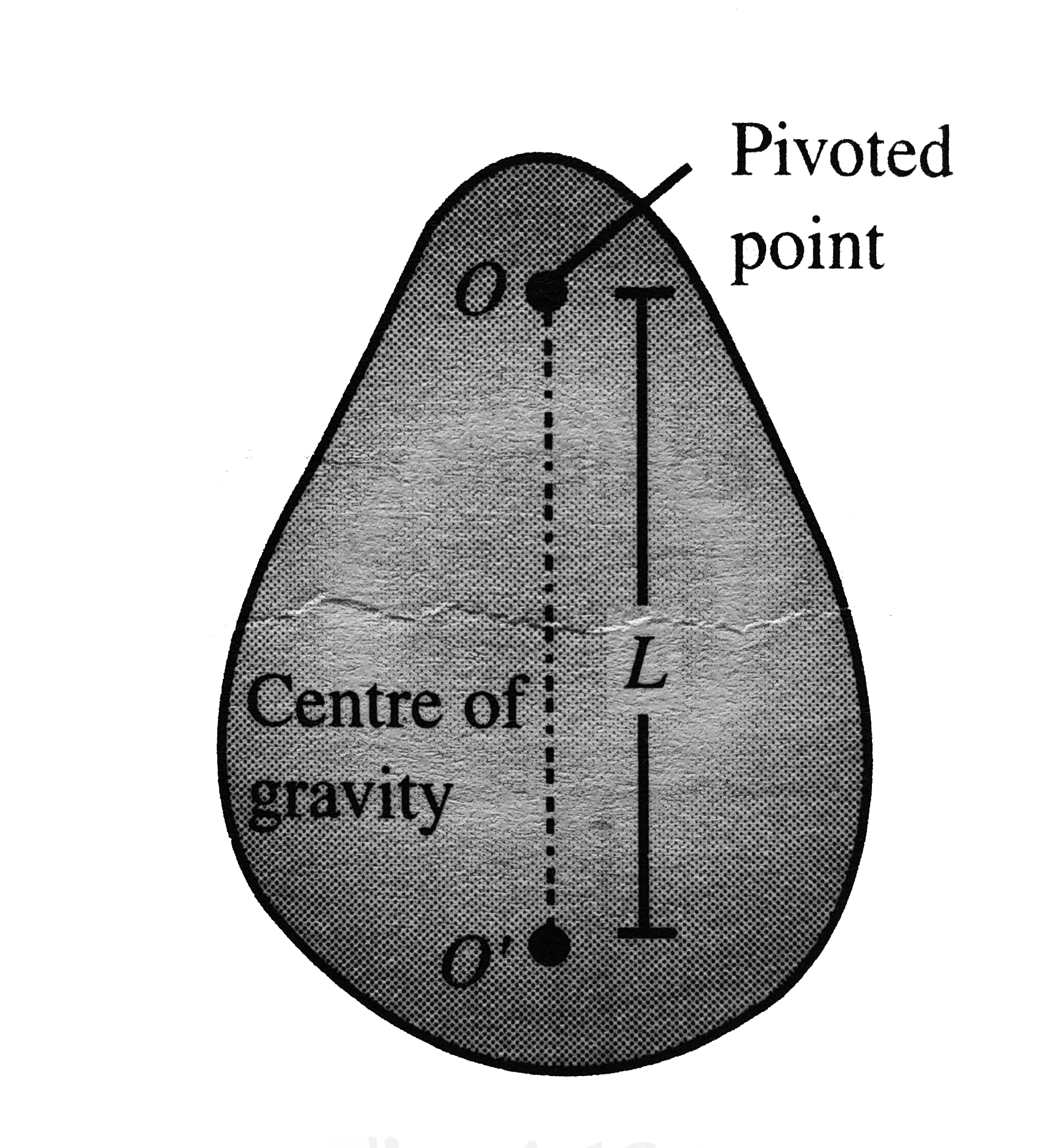
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.
View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .
View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. For the above question, locate the centre of oscillation.
View SolutionStatement-1 : During the oscillation so f a simple pendulum, the direction of its acceleration at the mean position is directed towards the point of suspension and at exteme position is direction towards the mean position .
Statement-2 : The directio of acceleration of a simple pendulum at an instant is decided by the tangential and radial components of weight at that instant.
View Solution