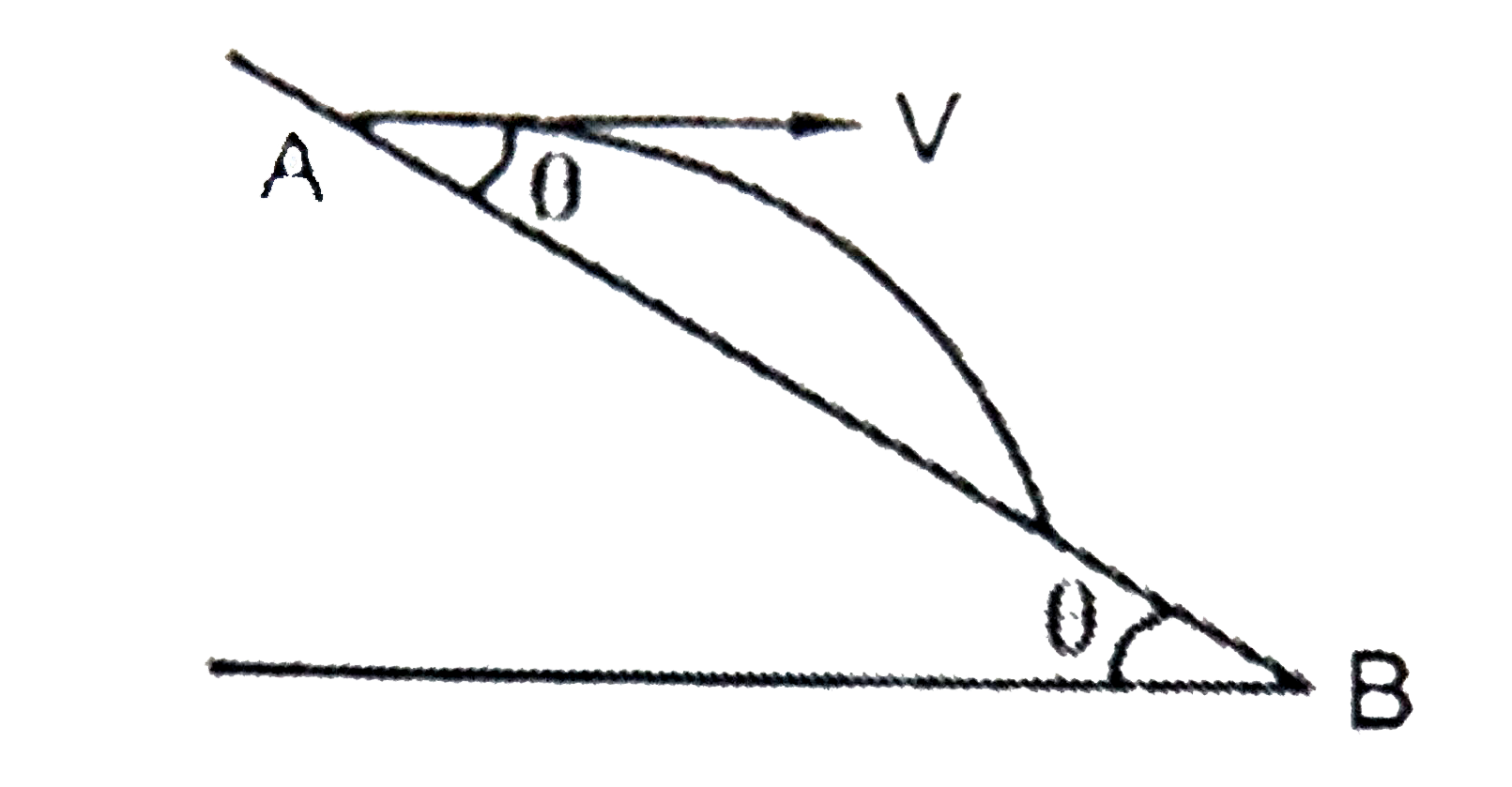
A particle is projected horizontal with a speed u from the top of plane inclined at an angle $θ$ with the horizontal. How far from the point of projection will the particle strike the plane?

Video Solution

Text Solution

Verified by Experts

Let us select point projection as the origin and X- and Y-axis as shown in the figure .

There is no acceleration in the horizontal direction hence we can write the following :
$x = ut \Rightarrow t \frac{x}{u}$
We can use $S = ut + \frac{1}{2} {at}^{2}$ in the Y-direction . Initial
Velocity along Y-axis is zero and acceleration a=g, as we have selected downward direction as the positive direction .
$S = ut + \frac{1}{2} {at}^{2}$
$\Rightarrow y = \frac{1}{2} {gt}^{2}$
Substituting t from equation (i) ,
$\Rightarrow y = \frac{1}{2} {g (\frac{x}{u})}^{2} \Rightarrow y = \frac{g x^{2}}{2 u^{2}}$
We can also write the following equation:
$y = x tan θ$
Substituting from equation (iii) in equation (ii) , we get the following :
$x tan θ = \frac{g x^{2}}{2 u^{2}}$
$\Rightarrow x = \frac{2 u^{2}}{g} tan θ$
Substituting in equation (iii) , we get the following :
$y = \frac{2 u^{2}}{g} {tan}^{2} θ$
Distance of the stone point of projection can be written as followings:
$l = \sqrt{x^{2} + y^{2}} = \frac{2 u^{2}}{g} tan θ \sqrt{1 + {tan}^{2} t h e a}$
$\Rightarrow l = \frac{2 u^{2}}{g} tan θ sec θ$

A ball is projected horizontally with a speed v from the top of the plane inclined at an angle $45^{\circ}$ with the horizontal. How far from the point of projection will the ball strikes the plane?
A $\frac{2 v^{2}}{g}$
B $\sqrt{2} [\frac{2 v^{2}}{g}]$
C $\frac{v^{2}}{g}$
D $\sqrt{2} \frac{v^{2}}{g}$
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle $θ = 37^{\circ}$ to the horizontal $(g = 10 m / s^{2})$

How far from the point of projection will the particle strike the plane?
A75m
B $\frac{65}{16} m$
C $\frac{75}{16} m$
D $\frac{85}{9} m$
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle $θ = 37^{\circ}$ to the horizontal $(g = 10 m / s^{2})$

Find the time taken by the particle to hit the plane.
A $\frac{3}{4} s$
B $3 s$
C $4 s$
D $\frac{4}{3} s$