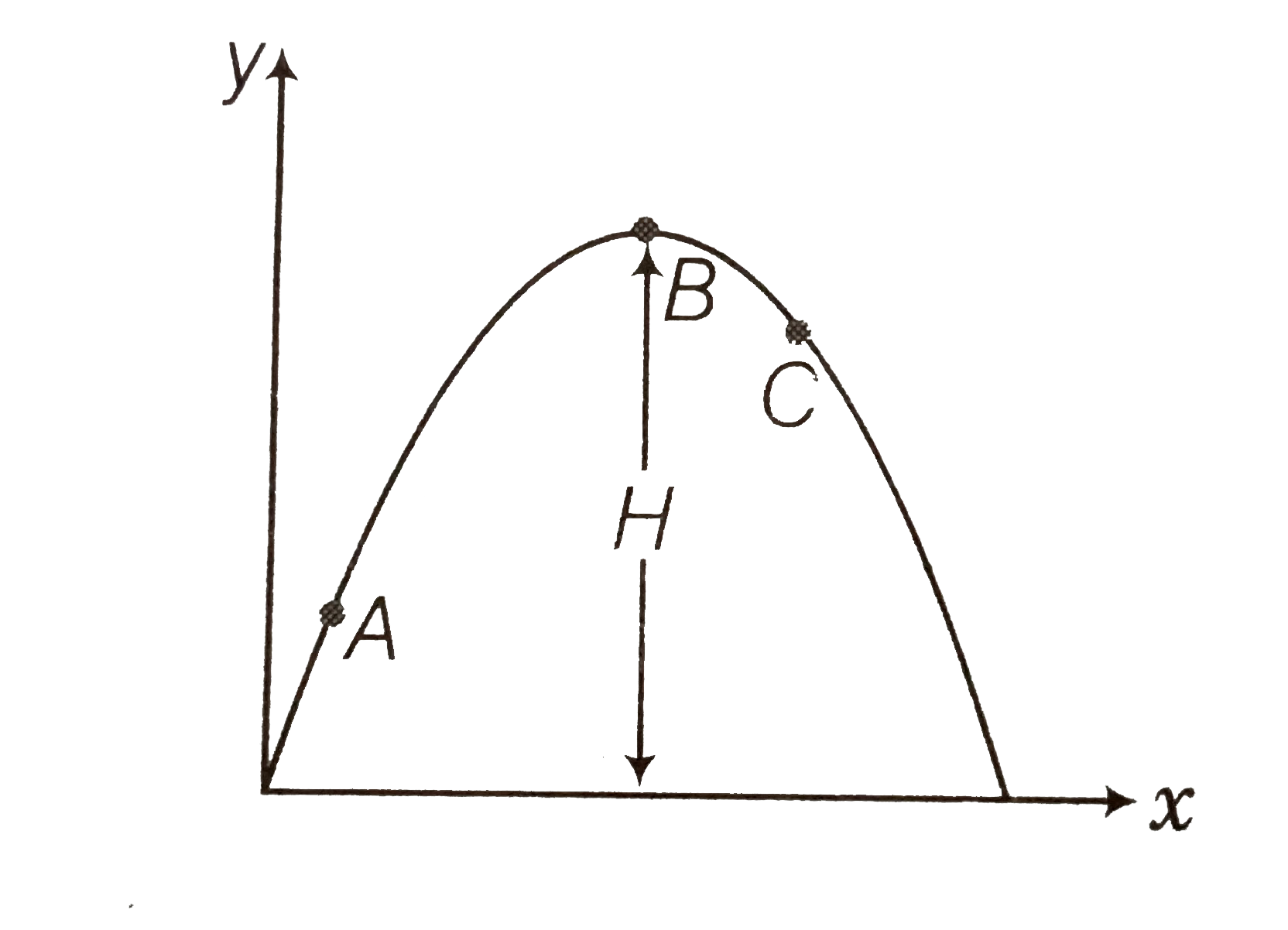
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure where x and y indicate horizontal and vertical directions, respectively . Shown in the diagram, direction of velocity and acceleration at points A, B and C.
Consider the adjacent diagram in which a particle is projected at an angle θ.
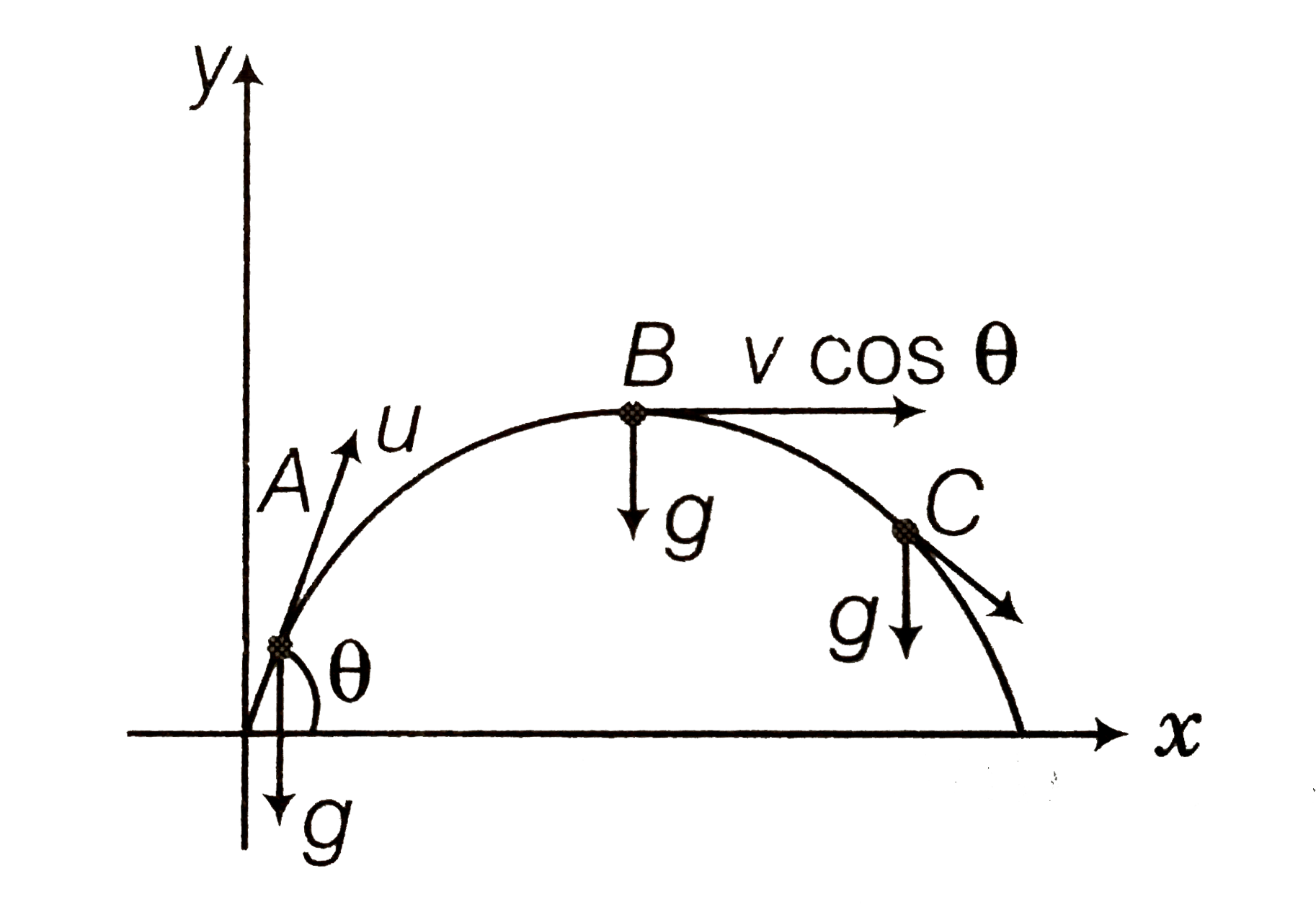
vx=Horizontal component of velocity = v cosθ=constant.
vy = Vertical component of velocity =vsinθ
Velocity will always be tangential to the curve in the direction of motion and acceleration is always vertically downward and is equal to g (acceleration due to gravity).
Topper's Solved these Questions
Similar Questions
A particle is projected from ground at some angle with horizontal (Assuming point of projection to the origin and the horizontal and vertical directions to be the x and y axis) the particle passes through the points (3, 4) m and (4, 3) m during its motion then the range of the particle would be : (g=10m/s2)
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected with an angle of projection θ to the horizontal line passing through the points (P,Q) and (Q,P) referred to horizontal and vertical axes (can be treated as X-axis and Y-axis respectively). The angle of projection can be given by
View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionWhen a particle is projected at some angle with the horizontal, the path of the particle is parabolic. In the process the horizontal velocity remains constant but the magnitude of vertical velocity changes. At any instant during flight the acceleration of the particle remains g in vertically downward direction. During flight at any point the path of particle can be considered as a part of circle and radius of that circle is called the radius of curvature of the path
Consider that a particle is projected with velocity u=10m/s at an angle θ=60∘ with the horizontal and take value of g=10m/s2. Now answer the following questions.
The radius of curvature of path of particle at the instant when the velocity vector of the particle becomes perpendicular to initial velocity vector is
View SolutionWhen a particle is projected at some angle with the horizontal, the path of the particle is parabolic. In the process the horizontal velocity remains constant but the magnitude of vertical velocity changes. At any instant during flight the acceleration of the particle remains g in vertically downward direction. During flight at any point the path of particle can be considered as a part of circle and radius of that circle is called the radius of curvature of the path
Consider that a particle is projected with velocity u=10m/s at an angle θ=60∘ with the horizontal and take value of g=10m/s2. Now answer the following questions.
The magnitude of acceleration of particle at that instant is
View SolutionWhen a particle is projected at some angle with the horizontal, the path of the particle is parabolic. In the process the horizontal velocity remains constant but the magnitude of vertical velocity changes. At any instant during flight the acceleration of the particle remains g in vertically downward direction. During flight at any point the path of particle can be considered as a part of circle and radius of that circle is called the radius of curvature of the path
Consider that a particle is projected with velocity u=10m/s at an angle θ=60∘ with the horizontal and take value of g=10m/s2. Now answer the following questions.
Tangential acceleration of particle at that instant is
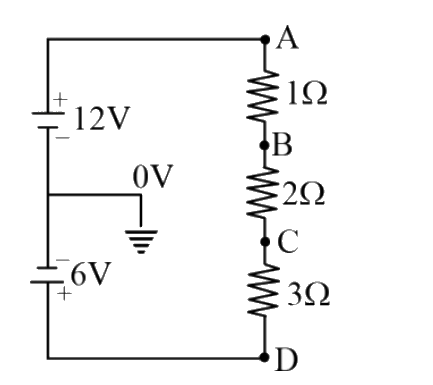
View SolutionIn the circuit diagram shown in Figure , the potentials of the points B, C and D are respectively -
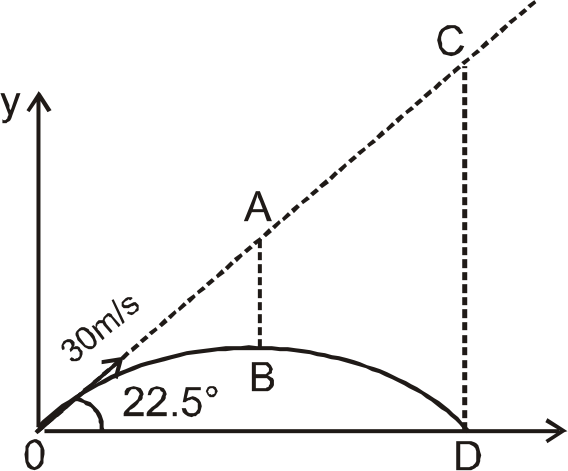
View SolutionA particle is projected with speed 30m/s at angle 22.5∘ with horizontal from ground as shown. AB and CD are parallel to y-axis and B is highest point of trajectory of particle. CD/AB is
View Solution
