A particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If aandb are the base angles of the triangle and θ the angle of projection, prove that tanθ=tan∝+tanβ.
Let ABC be the triangle with base BC. Let h be the height of the vertex A above BC. If AM is the perpendicular drawn on base BC from vertex A, then tan∝=h/a and tanβ=H/B, where BM=aandCM=b.
Since A(a,h) lies on the trajectory of the projectile,
y=xtanθ(1−xR) ...(i)
Therefore, it should satisfy (i) i.e.,
h=atanθ(1−aa+b)[∵Ran≥,R=a+b]
ha=tanθ[ba+b]
⇒tanθ=ha+hb=tan∝+tanβ
Hence, proved.
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples7videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.115videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ.
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View Solution
Knowledge Check
- Question 1 - Select One
A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If α,β are the base angles and θ the angle of projection, then
Atanθ=tanα−tanβBtanθ=tanβ−tanαCtanθ=tanα+tanβDNone of these - Question 2 - Select One
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is
A2√3B4√3C13D3 - Question 3 - Select One
A particle is projected at angle θ from horizontal. The product of the two possible times it take to pass over the height h(h<Hmax) is
A2ugB2hgC2usinθgDNone
A particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA projectile is fired from the base of cone shaped hill. The projectle grazes the vertex and strikes the hill again at the base. If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then tanθtanα is:
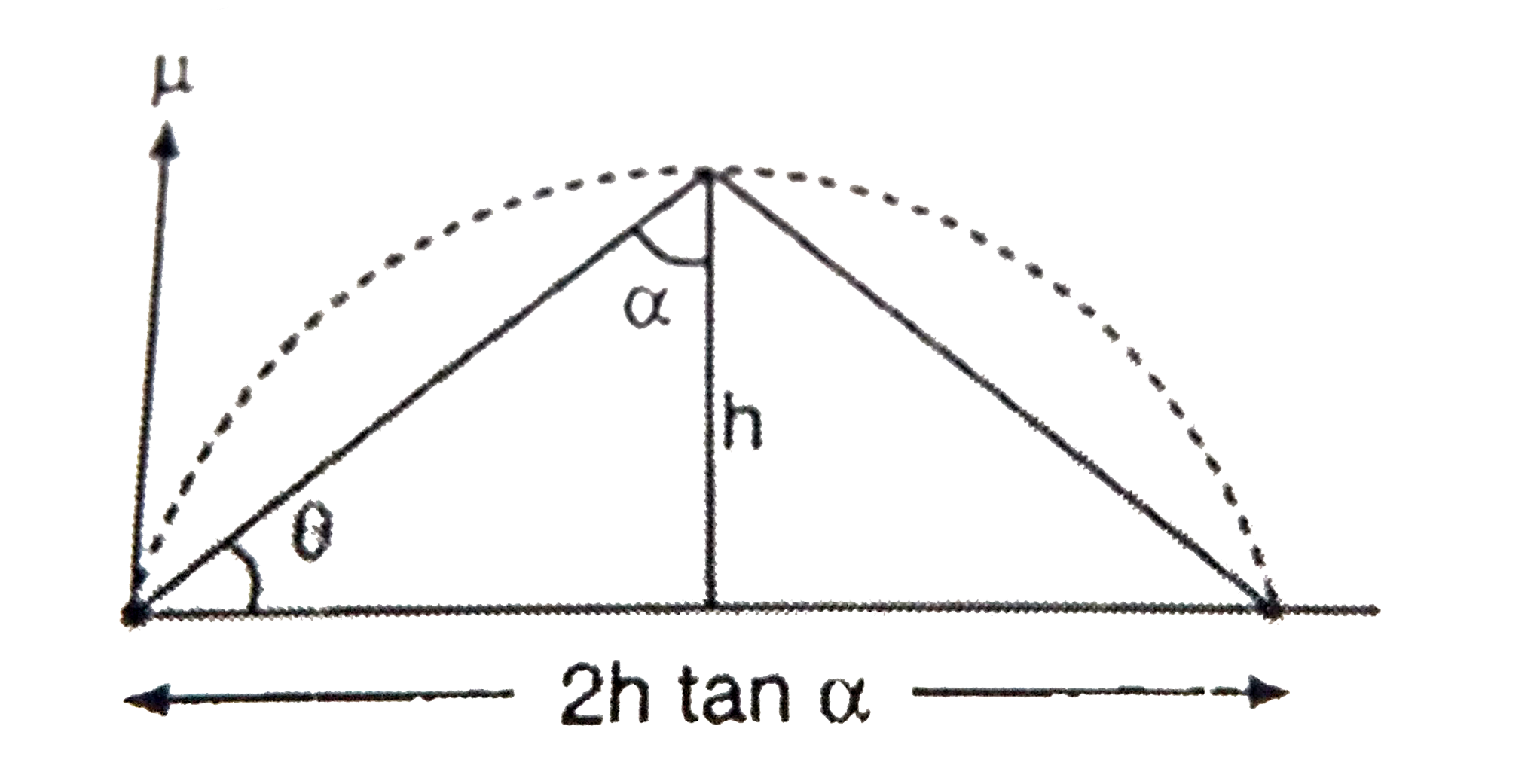 View Solution
View SolutionA projectile is fired from the base of coneshaped hill. The projectile grazes the vertex and strikes the hill again at the base.If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then then θtanθis
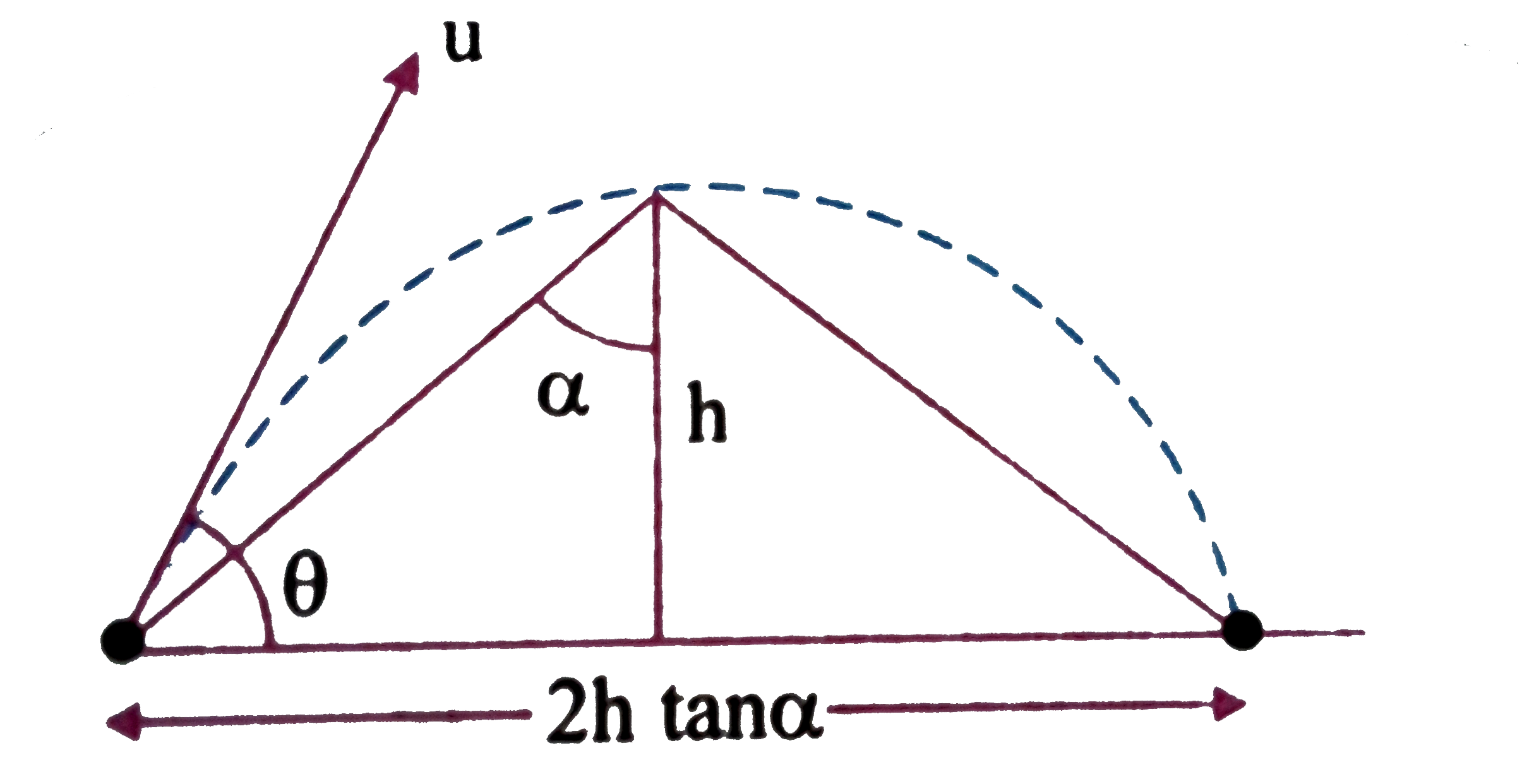 View Solution
View SolutionProve that the angle between internal bisector of one base angle and the external bisector of the other base angle of a triangle is equal to one half of the vertical angle.
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View Solution

