A particle moves in space along the path z=ax3+by2 in such a way that dxdt=c=dydt where a,b and c are constants. The acceleration of the particle is
(6ac2x+2bc2)ˆk
(2ax2+6by2)ˆk
(4bc2+3ac2)ˆk
(bc2x+2by)ˆk
The correct Answer is:A
To find the acceleration of the particle moving along the path z=ax3+by2, we will follow these steps:
Step 1: Understand the given information
We have the path equation:
z=ax3+by2
and the relationships:
dxdt=canddydt=c
where a,b, and c are constants.
Step 2: Differentiate the path equation with respect to time
To find the velocity in the z-direction, we differentiate z with respect to t:
dzdt=ddt(ax3+by2)
Using the chain rule:
dzdt=a⋅3x2dxdt+b⋅2ydydt
Step 3: Substitute the values of dxdt and dydt
Since dxdt=c and dydt=c, we substitute these into the equation:
dzdt=a⋅3x2⋅c+b⋅2y⋅c
Simplifying this gives:
dzdt=3acx2+2bc
Step 4: Differentiate again to find acceleration
Now, we differentiate dzdt with respect to t to find the acceleration:
d2zdt2=ddt(3acx2+2bc)
Using the product rule:
d2zdt2=3ac⋅2xdxdt+0
Substituting dxdt=c:
d2zdt2=6acx⋅c=6acx2
Step 5: Write the acceleration vector
The acceleration vector in the z-direction is:
a=d2zdt2^k=(6acx)^k
Final Answer
Thus, the acceleration of the particle is:
a=6acx^k
We have the path equation:
z=ax3+by2
and the relationships:
dxdt=canddydt=c
where a,b, and c are constants.
To find the velocity in the z-direction, we differentiate z with respect to t:
dzdt=ddt(ax3+by2)
Using the chain rule:
dzdt=a⋅3x2dxdt+b⋅2ydydt
Since dxdt=c and dydt=c, we substitute these into the equation:
dzdt=a⋅3x2⋅c+b⋅2y⋅c
Simplifying this gives:
dzdt=3acx2+2bc
Now, we differentiate dzdt with respect to t to find the acceleration:
d2zdt2=ddt(3acx2+2bc)
Using the product rule:
d2zdt2=3ac⋅2xdxdt+0
Substituting dxdt=c:
d2zdt2=6acx⋅c=6acx2
The acceleration vector in the z-direction is:
a=d2zdt2^k=(6acx)^k
Thus, the acceleration of the particle is:
a=6acx^k
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A particle moves along a path y=ax2 (where a is constant) in such a way that x-component of its velocity (ux) remains constant. The acceleration of the particle is
View SolutionA particle of mass m moves along a curve y=x2. When particle has x-coordinate as 12 m and x-component of velocity as 4ms, then
View SolutionThe velocity υ of a particle as a function of its position (x) is expressed as υ=√c1−c2x, where c1 and c2 are positive constants. The acceleration of the particle is
View SolutionA particle moves in a circular path such that its speed v varies with distance as V=α√s where α is a positive constant. Find the acceleration of the particle after traversing a distance s.
View SolutionA particle moves in a circular path such that its speed 1v varies with distance s as v=√s, where ∝ is a positive constant. Find the acceleration of the particle after traversing a distance s.
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance S as K=βS2 , where β is a constant. Tangential acceleration of the particle is proportional to
View SolutionA particle moves in a circular path such that its speed v varies with distance as v=α√s where α is a positive constant. Find the acceleration of particle after traversing a distance S?
View SolutionA particle moves along the parabola y2=2ax in such a way that its projection on y-axis has a constant velocity. Show that its projection on the x-axis moves with constant acceleration
View SolutionA particle moving with a uniform acceleration along a straight line covers distances a and b in successive intervals of p and q second. The acceleration of the particle is
View SolutionA particle moves along a constant curvature path between A and B (length of curve wire AB is 100m) with a constant speed of 72km/hr. The acceleration of particle at mid point 'C' of curve AB is
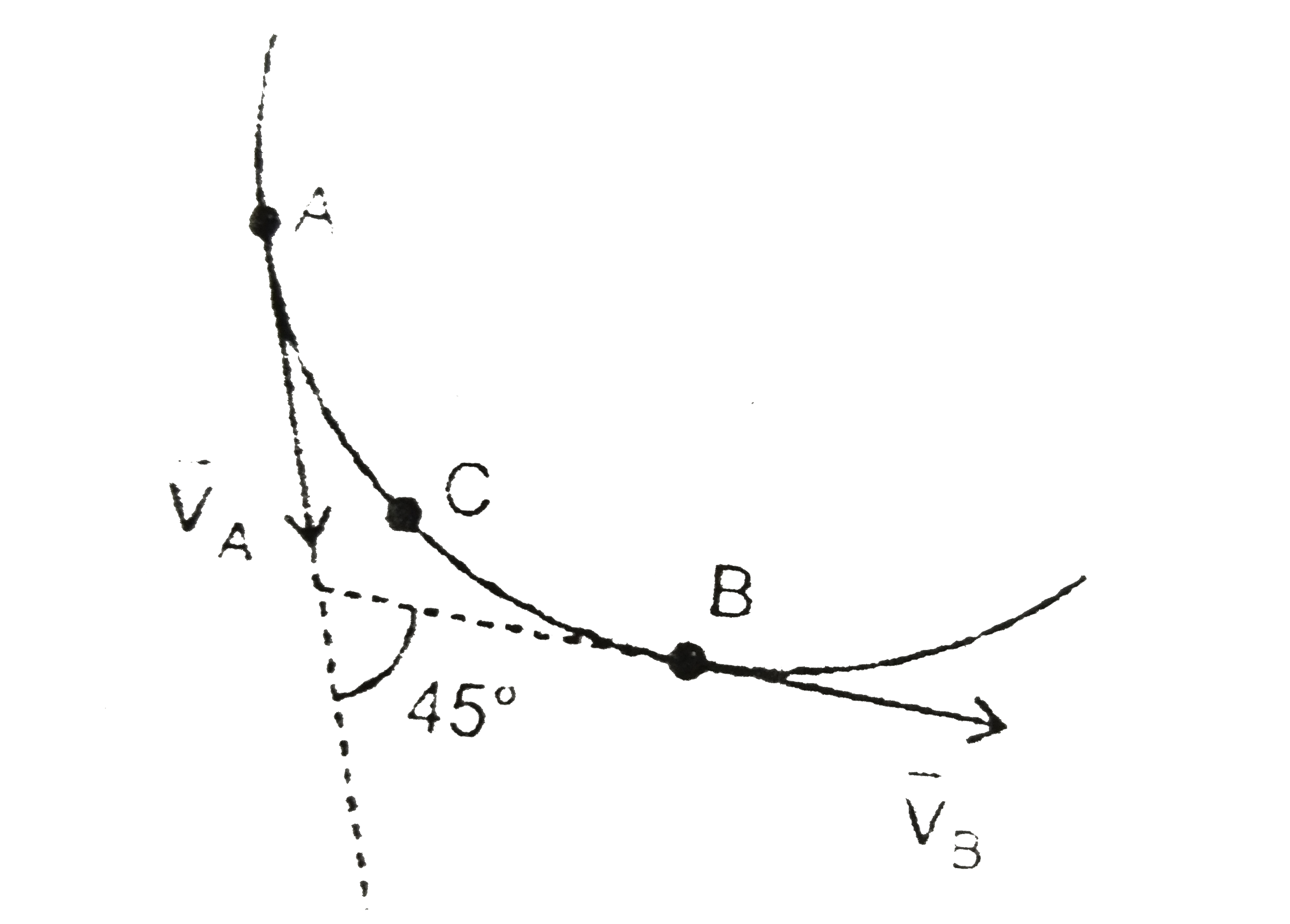
View Solution
