A particle moving with a uniform acceleration along a straight line covers distances a and b in successive intervals of p and q second. The acceleration of the particle is
pq(p+q)2(dp−aq)
2(aq−dp)pq(p−q)
bp−aqpq(p−q)
2(bp−aq)pq(p+q)
The correct Answer is:D
To find the acceleration of a particle moving with uniform acceleration while covering distances a and b in successive intervals of p and q seconds, we can use the equations of motion. Here’s a step-by-step solution:
Step 1: Write the equations of motion for the first interval
For the first interval where the particle covers distance a in time p, we use the equation of motion:
s=ut+12at2
Substituting the known values:
a=up+12ap2(Equation 1)
Step 2: Write the equations of motion for the second interval
For the second interval where the particle covers distance b in time q, we first need to find the initial velocity at the start of this interval. The final velocity v at the end of the first interval is given by:
v=u+at
Substituting for t=p:
v=u+ap(Equation 2)
Now, using this velocity as the initial velocity for the second interval, we write the equation for distance b:
b=vq+12aq2
Substituting v from Equation 2:
b=(u+ap)q+12aq2
Expanding this gives:
b=uq+apq+12aq2(Equation 3)
Step 3: Rearranging the equations
From Equation 1:
a=up+12ap2⟹a−12ap2=up⟹a(1−12p2)=up
From Equation 3:
b=uq+apq+12aq2⟹b−uq=apq+12aq2
Rearranging gives:
b−uq=a(pq+12q2)(Equation 4)
Step 4: Multiply and simplify
Now, multiply Equation 1 by q and Equation 3 by p:
aq=upq+12aqp2(Equation 5)
bp=uq+apq+12aq2(Equation 6)
Step 5: Subtract Equation 6 from Equation 5
Now, subtract Equation 6 from Equation 5:
aq−bp=upq−uq+12aqp2−apq−12aq2
This simplifies to:
aq−bp=(upq−uq)+12a(p2−q2)
Step 6: Solve for acceleration a
Rearranging gives:
aq−bp=upq−uq+12a(p2−q2)
Now, isolate a:
a(qp−12(p2−q2))=upq−uq
Thus,
a=upq−uqqp−12(p2−q2)
Final Expression for Acceleration
The acceleration a can be expressed as:
a=2(bp−aq)pq(p+q)
For the first interval where the particle covers distance a in time p, we use the equation of motion:
s=ut+12at2
Substituting the known values:
a=up+12ap2(Equation 1)
For the second interval where the particle covers distance b in time q, we first need to find the initial velocity at the start of this interval. The final velocity v at the end of the first interval is given by:
v=u+at
Substituting for t=p:
v=u+ap(Equation 2)
Now, using this velocity as the initial velocity for the second interval, we write the equation for distance b:
b=vq+12aq2
Substituting v from Equation 2:
b=(u+ap)q+12aq2
Expanding this gives:
b=uq+apq+12aq2(Equation 3)
From Equation 1:
a=up+12ap2⟹a−12ap2=up⟹a(1−12p2)=up
From Equation 3:
b=uq+apq+12aq2⟹b−uq=apq+12aq2
Rearranging gives:
b−uq=a(pq+12q2)(Equation 4)
Now, multiply Equation 1 by q and Equation 3 by p:
aq=upq+12aqp2(Equation 5)
bp=uq+apq+12aq2(Equation 6)
Now, subtract Equation 6 from Equation 5:
aq−bp=upq−uq+12aqp2−apq−12aq2
This simplifies to:
aq−bp=(upq−uq)+12a(p2−q2)
Rearranging gives:
aq−bp=upq−uq+12a(p2−q2)
Now, isolate a:
a(qp−12(p2−q2))=upq−uq
Thus,
a=upq−uqqp−12(p2−q2)
The acceleration a can be expressed as:
a=2(bp−aq)pq(p+q)
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)
19 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 1
75 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
A body moving in a straight line with constant acceleration covers distances a and b in successive equal time interval of t. The acceleration of the body is
View SolutionA particle, moving with uniform acceleration along a straight line ABC, crosses point A at t = 0 with a velocity 12 m/s. B is 40 m from A and C is 64 m from A. The particle passes B at t = 4 s.
(a) At what time, will the particle be C?
(b) What is its velocity at C?
View SolutionShow that when a particle moves with uniform acceleration , the distances described in consecutive equal intervals of time are in A.P.
View SolutionA particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
 .
.
View SolutionA body moving with uniform acceleration a straight line describes 25m in the fifth second and 33m in the seventh second. Find its initial velocity and acceleration.
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionA body is moving with variable acceleartion (a) along a straight line. The average acceleration of body in time interval t1 to t2 is :-
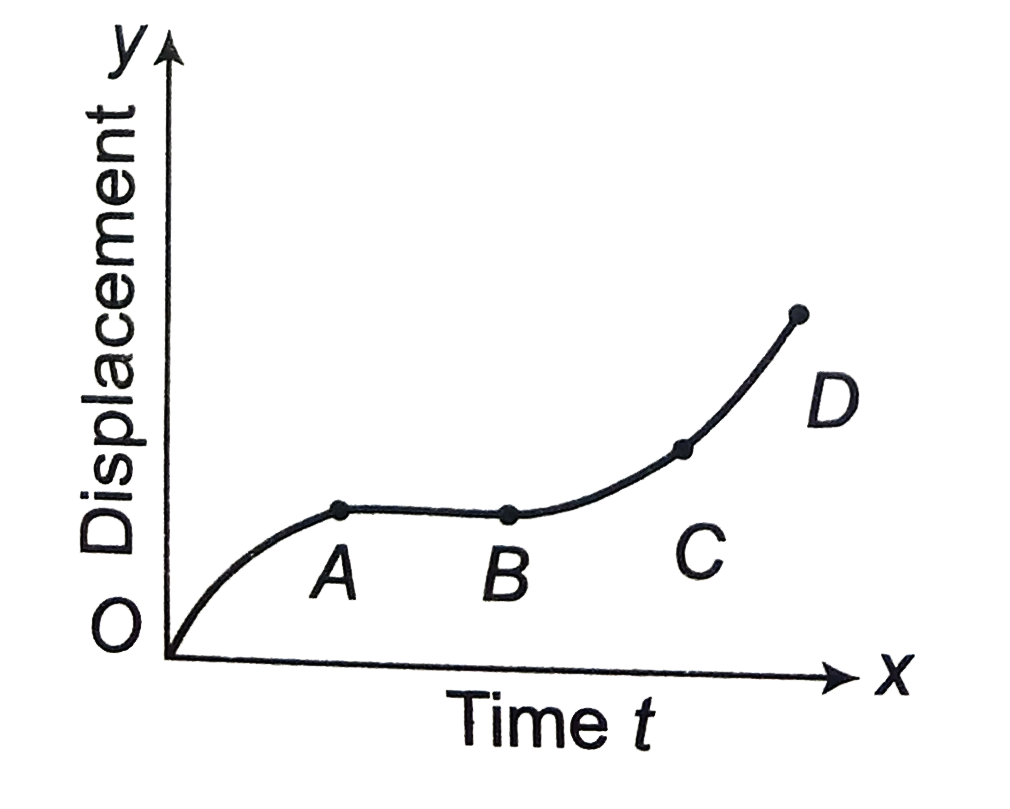
View SolutionThe graph between the displacement x and time t for a particle moving in a straight line is shown in the figure. During the interval OA,AB,BC and CD the acceleration of the particle is
OA,AB,BC,CD
View SolutionDisplacement-time curve of a particle moving along a straight line is shown. Tangents at A and B makes angle 45∘ and 135∘ with positive x-axis respectively. The average acceleration of the particle during t=1,t=2 seconds is

View SolutionA particle moves with constant acceleration along a straight line streaming from rest. The percentage increase in its displacement during the 4th second compared to that in the 3rd second is
View Solution
