A particle moves along a constant curvature path between A and B (length of curve wire AB is 100m) with a constant speed of 72km/hr. The acceleration of particle at mid point 'C' of curve AB is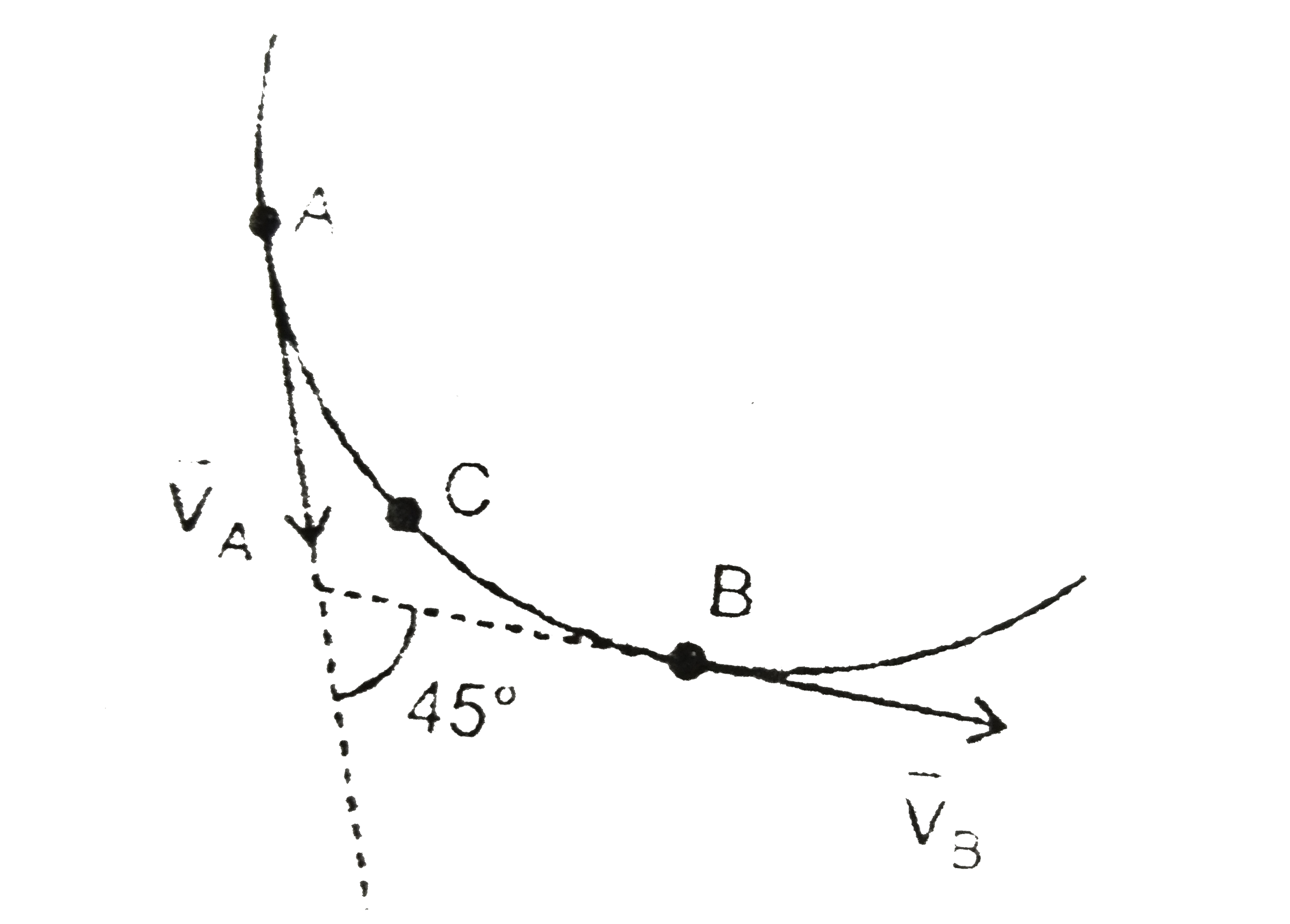 
The correct Answer is:B
aC=|¯v|2R=(20)2400π=πm/s2
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A particle moves along a path y=ax2 (where a is constant) in such a way that x-component of its velocity (ux) remains constant. The acceleration of the particle is
View SolutionA particle is revoiving in a circular path of radius 25 m with constant angular speed 12 rev/min. then the angular acceleration of particle is
View SolutionA particle is moving on a circular path with constant speed, then its acceleration will be constant in
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
View SolutionA particle describes an angle θ in a circular path with a constant speed v. Find the a charge in the velocity of the particle and b average acceleration of the particle during the motion in the curve (circle).
.
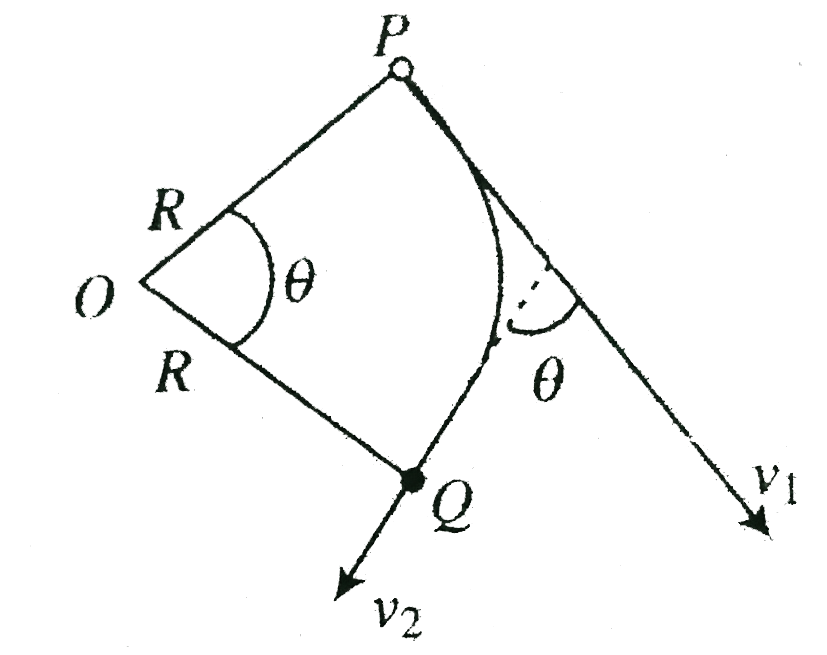View SolutionA particle moves along a straight line path. After some time it comes to rest. The motion is with constant acceleration whose direction with respect to the direction of velocity is :
View SolutionA particle moves along a straight line path. After some time it comes to rest. The motion is with constant acceleration whose direction with respect to the direction of velocity is :
View Solution