A particle moves under the action of a force F=20ˆi+15ˆj along a straight line 3y+αx=5, where, α is a constant. If the work done by the force F is zero the value of α is .
49
94
3
4
The correct Answer is:D
To solve the problem, we need to find the value of the constant α such that the work done by the force F=20^i+15^j is zero while the particle moves along the line defined by 3y+αx=5.
1. Understanding the Condition for Zero Work Done:
The work done by a force is given by the dot product of the force vector and the displacement vector. For the work done to be zero, the force must be perpendicular to the direction of motion. This means that the angle θ between the force vector F and the direction of motion must be 90∘.
2. Finding the Direction of the Force:
The force vector is given by:
F=20^i+15^j
The slope of the force vector can be calculated as:
tanθ1=FyFx=1520=34
3. Finding the Slope of the Line:
The equation of the line is given by:
3y+αx=5
Rearranging this into the slope-intercept form y=mx+b:
y=−α3x+53
The slope m of the line is:
tanθ2=−α3
4. Setting Up the Perpendicular Condition:
For the two vectors (the force and the direction of motion) to be perpendicular, the product of their slopes must equal −1:
tanθ1⋅tanθ2=−1
Substituting the values we found:
(34)(−α3)=−1
5. Solving for α:
Simplifying the equation:
−3α12=−1
This simplifies to:
α4=1
Therefore:
α=4
Conclusion:
The value of α is 4.
The work done by a force is given by the dot product of the force vector and the displacement vector. For the work done to be zero, the force must be perpendicular to the direction of motion. This means that the angle θ between the force vector F and the direction of motion must be 90∘.
The force vector is given by:
F=20^i+15^j
The slope of the force vector can be calculated as:
tanθ1=FyFx=1520=34
The equation of the line is given by:
3y+αx=5
Rearranging this into the slope-intercept form y=mx+b:
y=−α3x+53
The slope m of the line is:
tanθ2=−α3
For the two vectors (the force and the direction of motion) to be perpendicular, the product of their slopes must equal −1:
tanθ1⋅tanθ2=−1
Substituting the values we found:
(34)(−α3)=−1
Simplifying the equation:
−3α12=−1
This simplifies to:
α4=1
Therefore:
α=4
The value of α is 4.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
View SolutionA particle of mass 2kg travels along a straight line with velocity v=a√x, where a is a constant. The work done by net force during the displacement of particle from x=0 to x=4m is
View SolutionForces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
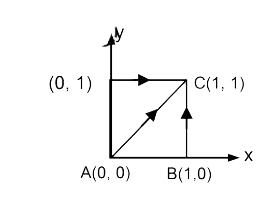
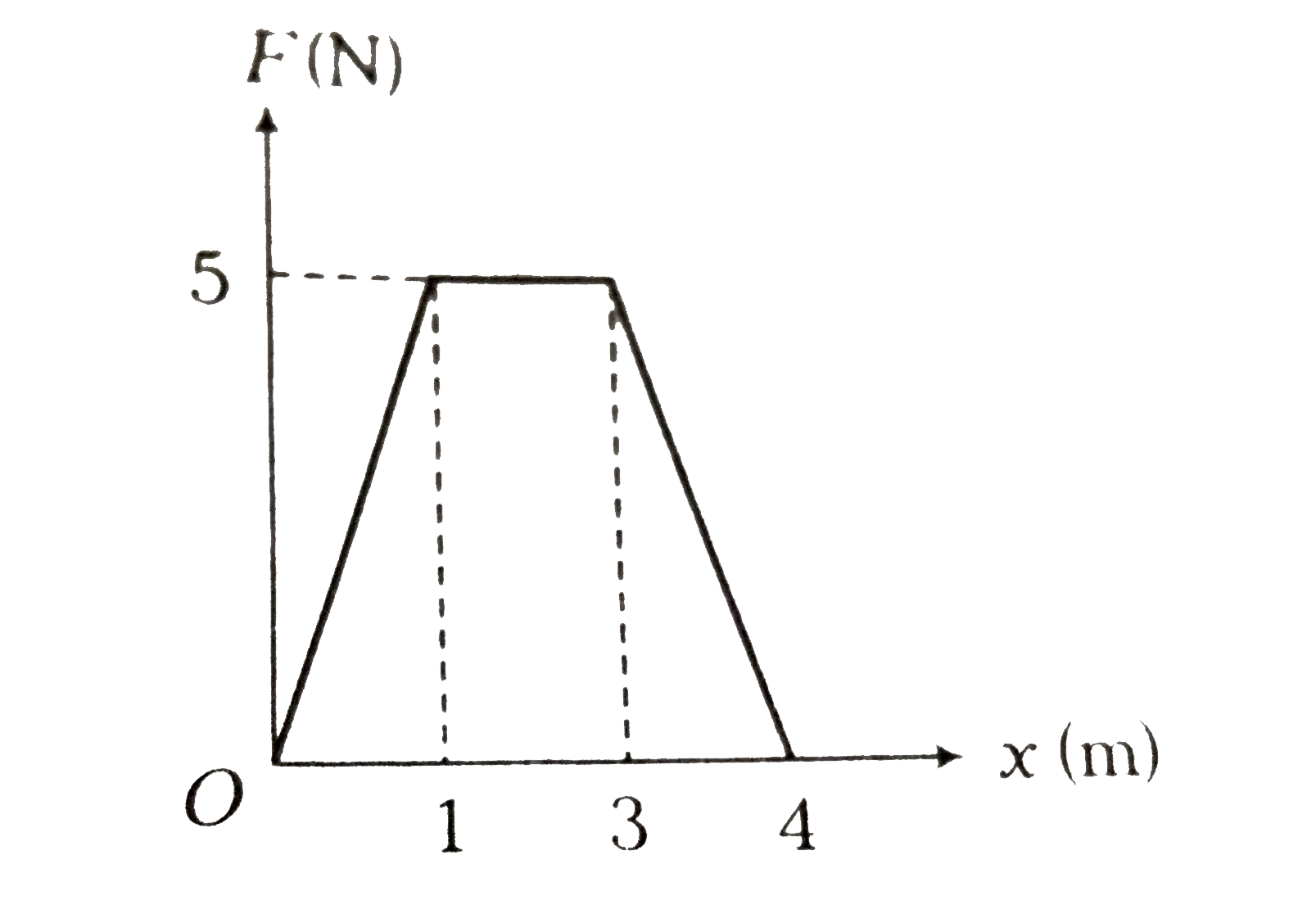
View SolutionThe force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
View SolutionA body moves under the action of a constant force along a straight line. The instantaneous power developed by this force with time t is correctly represented by.
View SolutionA particle moves from a point (2m,3m,0) to (3m,2m,0) under the action of force of magnitude 5N acting along the line y=x. The work done by the force on the particle during the displacement is
View SolutionA block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
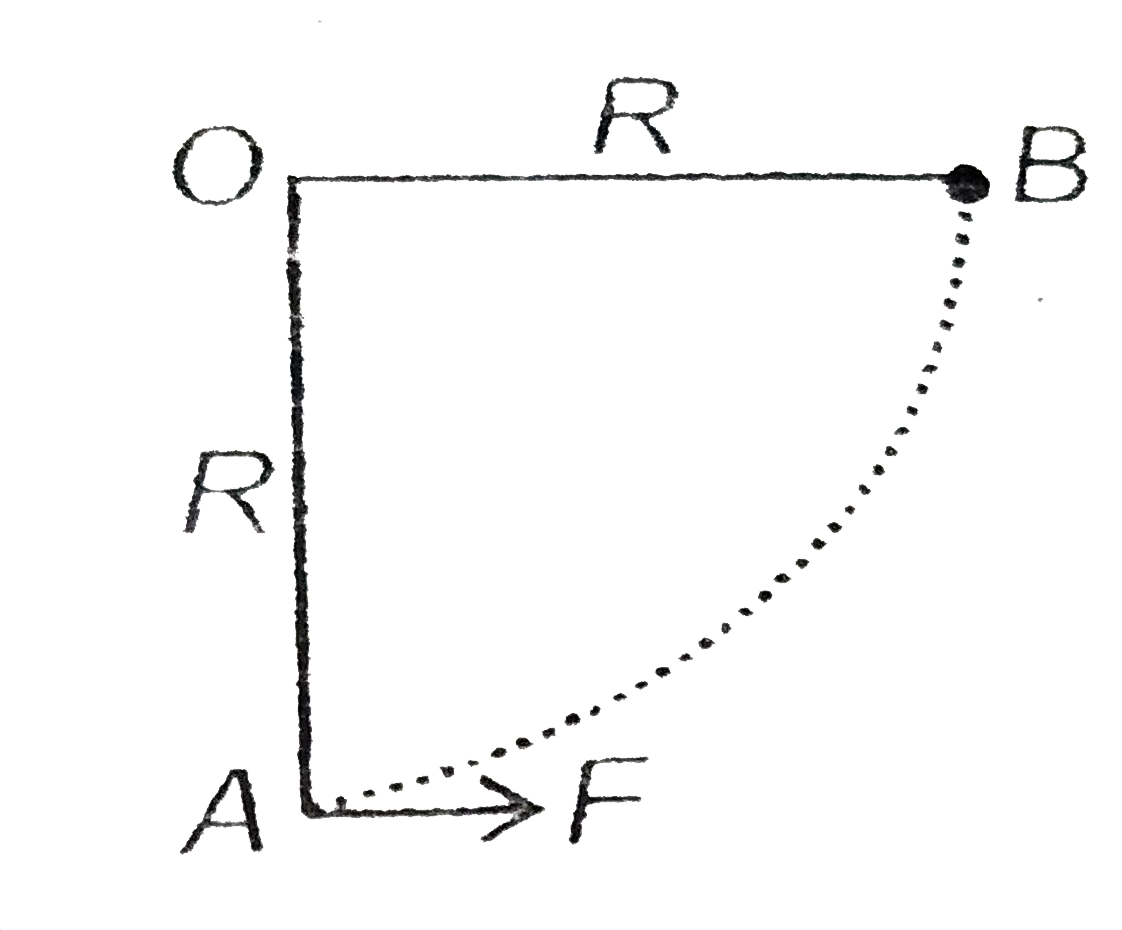
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View SolutionA particle is moving along x-axis under the action of a force, F which varies with its position (x) as F∝x−1/4. The variation of power due to this force with x is
View Solution
