A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision what could be minimum and the maximum value of u.
minimum value of v is 2 m/s
maximum value of v is 4 m/s
minimum value of v is 3 m/s
maximum value of v is 6 m/s
To solve the problem, we need to determine the minimum and maximum initial speed u of a particle of mass 100 g (0.1 kg) that collides with another particle of the same mass at rest, resulting in a total kinetic energy of 0.2 J after the collision.
1. Understand the Problem:
- We have two particles, each of mass m=0.1 kg.
- The first particle is moving with an initial speed u.
- The second particle is at rest.
- After the collision, the total kinetic energy is 0.2 J.
2. Calculate Initial Kinetic Energy:
- The initial kinetic energy (KE_initial) of the moving particle is given by:
KEinitial=12mu2
- Substituting m=0.1 kg:
KEinitial=12×0.1×u2=0.05u2
3. Determine the Change in Kinetic Energy:
- The change in kinetic energy (ΔKE) is the difference between the initial and final kinetic energy:
ΔKE=KEinitial−KEfinal
- Given that KEfinal=0.2 J, we have:
ΔKE=0.05u2−0.2
4. Consider Elastic and Inelastic Collisions:
- For elastic collisions, the coefficient of restitution e=1 and there is no loss of kinetic energy, so ΔKE=0.
- For perfectly inelastic collisions, e=0 and the maximum loss of kinetic energy occurs.
5. Set Up Equations for Elastic Collision:
- For elastic collision:
0.05u2−0.2=0⟹0.05u2=0.2⟹u2=0.20.05=4⟹u=2 m/s
6. Set Up Equations for Inelastic Collision:
- For perfectly inelastic collision, the two particles stick together and move with a common velocity V:
- By conservation of momentum:
mu=(m+m)V⟹0.1u=0.2V⟹V=u2
- The final kinetic energy is:
KEfinal=12(2m)V2=12(0.2)(u2)2=0.1u24=0.025u2
- Set this equal to the given final kinetic energy:
0.025u2=0.2⟹u2=0.20.025=8⟹u=2√2 m/s
7. Conclusion:
- The minimum value of u (for elastic collision) is 2 m/s.
- The maximum value of u (for inelastic collision) is 2√2 m/s.
Final Answer:
- Minimum value of u=2 m/s
- Maximum value of u=2√2 m/s
- We have two particles, each of mass m=0.1 kg.
- The first particle is moving with an initial speed u.
- The second particle is at rest.
- After the collision, the total kinetic energy is 0.2 J.
- The initial kinetic energy (KE_initial) of the moving particle is given by:
KEinitial=12mu2
- Substituting m=0.1 kg:
KEinitial=12×0.1×u2=0.05u2
- The change in kinetic energy (ΔKE) is the difference between the initial and final kinetic energy:
ΔKE=KEinitial−KEfinal
- Given that KEfinal=0.2 J, we have:
ΔKE=0.05u2−0.2
- For elastic collisions, the coefficient of restitution e=1 and there is no loss of kinetic energy, so ΔKE=0.
- For perfectly inelastic collisions, e=0 and the maximum loss of kinetic energy occurs.
- For elastic collision:
0.05u2−0.2=0⟹0.05u2=0.2⟹u2=0.20.05=4⟹u=2 m/s
- For perfectly inelastic collision, the two particles stick together and move with a common velocity V:
- By conservation of momentum:
mu=(m+m)V⟹0.1u=0.2V⟹V=u2
- The final kinetic energy is:
KEfinal=12(2m)V2=12(0.2)(u2)2=0.1u24=0.025u2
- Set this equal to the given final kinetic energy:
0.025u2=0.2⟹u2=0.20.025=8⟹u=2√2 m/s
- The minimum value of u (for elastic collision) is 2 m/s.
- The maximum value of u (for inelastic collision) is 2√2 m/s.
- Minimum value of u=2 m/s
- Maximum value of u=2√2 m/s
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
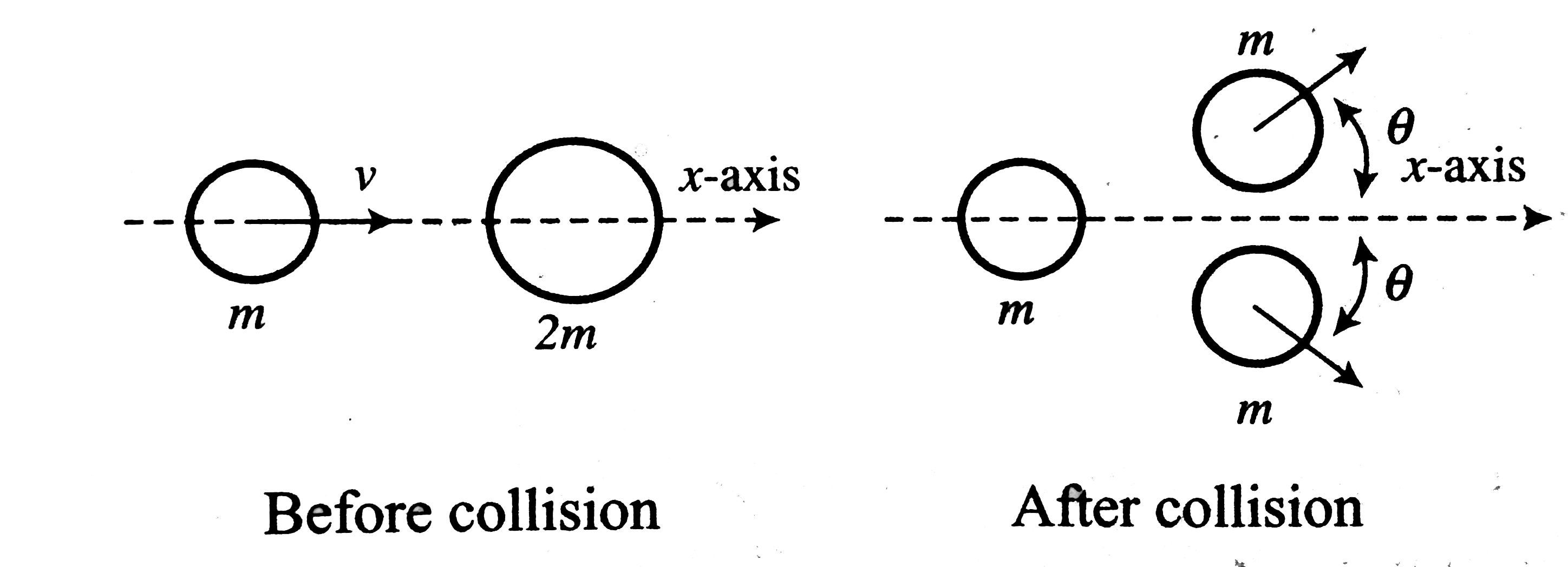
View SolutionA particle of mass m is moving along the x-axis with speed v when It collides with a particle of mass 2m initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? (θ>0)
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionA body of mass m1 moving at a constant speed undergoes an elastic head on collision with a body of mass m2 initially at rest. The ratio of the kinetic energy of mass m1 after the collision to that before the collision is -
View SolutionIf one sphere collides head - on with another sphere of the same mass at rest inelastically. The ratio of their speeds (v2v1) after collision shall be
View SolutionOn a friction surface a block a mass M moving at speed v collides elastic with another block of same mass M which is initially at rest . After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block's speed after the collision is
View SolutionA body of mass 2 m moving with velocity v makes a head - on elastic collision with another body of mass m which is initially at rest. Loss of kinetic energy of the colliding body (mass 2 m) is
View Solution
