A particle of mass in is made to move with uniform speed v0 along the perimeter of a regular hexagon, inscribed in a circle of radius R. The magnitude of impulse applied at each corner of the hexagon is
2mv0sinπ6
mv0sinπ6
mv0sinπ3
2mv0sinπ3
The correct Answer is:A
To solve the problem of finding the magnitude of impulse applied at each corner of a regular hexagon when a particle of mass m moves with uniform speed v0, we can follow these steps:
1. Understanding the Motion:
The particle moves along the perimeter of a regular hexagon inscribed in a circle of radius R. The corners of the hexagon are the points where the direction of the particle's velocity changes.
2. Identifying the Change in Momentum:
Impulse is defined as the change in momentum. When the particle reaches a corner, its velocity changes direction, but its speed remains constant. The change in momentum can be expressed as:
Δ→p=m→vfinal−m→vinitial
3. Calculating the Initial and Final Velocities:
At each corner of the hexagon, the particle's velocity changes direction by 60∘ (since the internal angle of a regular hexagon is 120∘, the external angle is 60∘). If we denote the initial velocity vector as →vinitial and the final velocity vector as →vfinal, we can express them in terms of their magnitudes and angles.
4. Using the Law of Cosines:
The magnitude of the change in momentum can be calculated using the law of cosines:
|Δ→p|=m√|→vinitial|2+|→vfinal|2−2|→vinitial||→vfinal|cos(60∘)
Since |→vinitial|=|→vfinal|=v0:
|Δ→p|=m√v20+v20−2v20⋅12=m√2v20−v20=m√v20=mv0
5. Final Expression for Impulse:
The magnitude of impulse I applied at each corner is equal to the change in momentum:
I=|Δ→p|=mv0
Conclusion:
The magnitude of impulse applied at each corner of the hexagon is mv0.
The particle moves along the perimeter of a regular hexagon inscribed in a circle of radius R. The corners of the hexagon are the points where the direction of the particle's velocity changes.
Impulse is defined as the change in momentum. When the particle reaches a corner, its velocity changes direction, but its speed remains constant. The change in momentum can be expressed as:
Δ→p=m→vfinal−m→vinitial
At each corner of the hexagon, the particle's velocity changes direction by 60∘ (since the internal angle of a regular hexagon is 120∘, the external angle is 60∘). If we denote the initial velocity vector as →vinitial and the final velocity vector as →vfinal, we can express them in terms of their magnitudes and angles.
The magnitude of the change in momentum can be calculated using the law of cosines:
|Δ→p|=m√|→vinitial|2+|→vfinal|2−2|→vinitial||→vfinal|cos(60∘)
Since |→vinitial|=|→vfinal|=v0:
|Δ→p|=m√v20+v20−2v20⋅12=m√2v20−v20=m√v20=mv0
The magnitude of impulse I applied at each corner is equal to the change in momentum:
I=|Δ→p|=mv0
The magnitude of impulse applied at each corner of the hexagon is mv0.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A particle of mass m is made to move with uniform speed u along the perimeter of a regular polygon of n sides. What is the magnitude of impulse applied by the particle at each corner of the polygon?
View SolutionA particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View Solution
Knowledge Check
Shown below is a regular hexagon inscribed in a circle whose radius is 4 inches . What is the perimeter, in inches, of the hexagon?
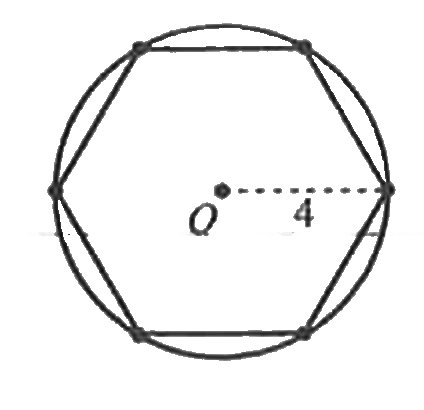 A8πB12√3C18D24
A8πB12√3C18D24
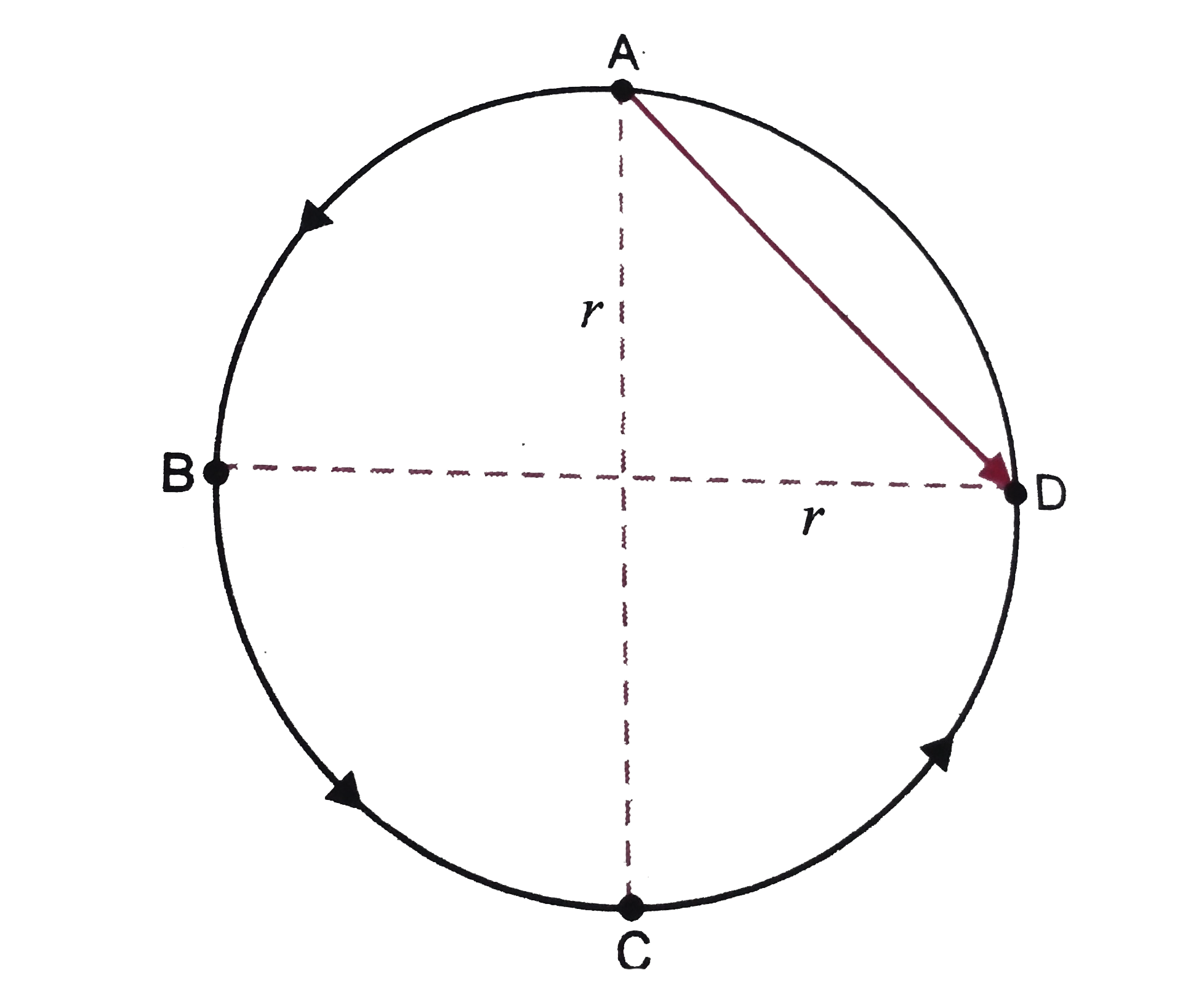
A particle moves over three quarters of a circle of radius r. What is the magnitude of its displacement ?
View SolutionA particle is moving with speed v in a circle of radius R. Find the magnitude for average velocity of point
for the half revolution
View SolutionA particle is moving in a circle with uniform speed v . In moving from a point to another diametrically opposite point
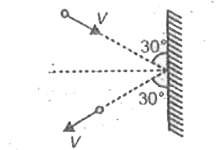
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View SolutionThe acceleration of an object moving in a circle of radius R with uniform speed v is
View SolutionA particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View Solution
