A particle of mass m comes down on a smooth inclined plane from point B at a height of h from rest. The magni-tude of change in momentum of the particle between position A (just before arriving on horizontal surface) and C (assuming the angle of inclination of the plane as θ with respect to the horizontal) is

0
2m√(2gh)sinθ
2m√(2gh)sin(θ2)
2m√(2gh)
The correct Answer is:C
The velocity of the particle when it reaches point A from B is
v=√(2gh) (directed along BA)
(pi)x=mvcosθ………..i
(pi)x=mvcosθ……ii
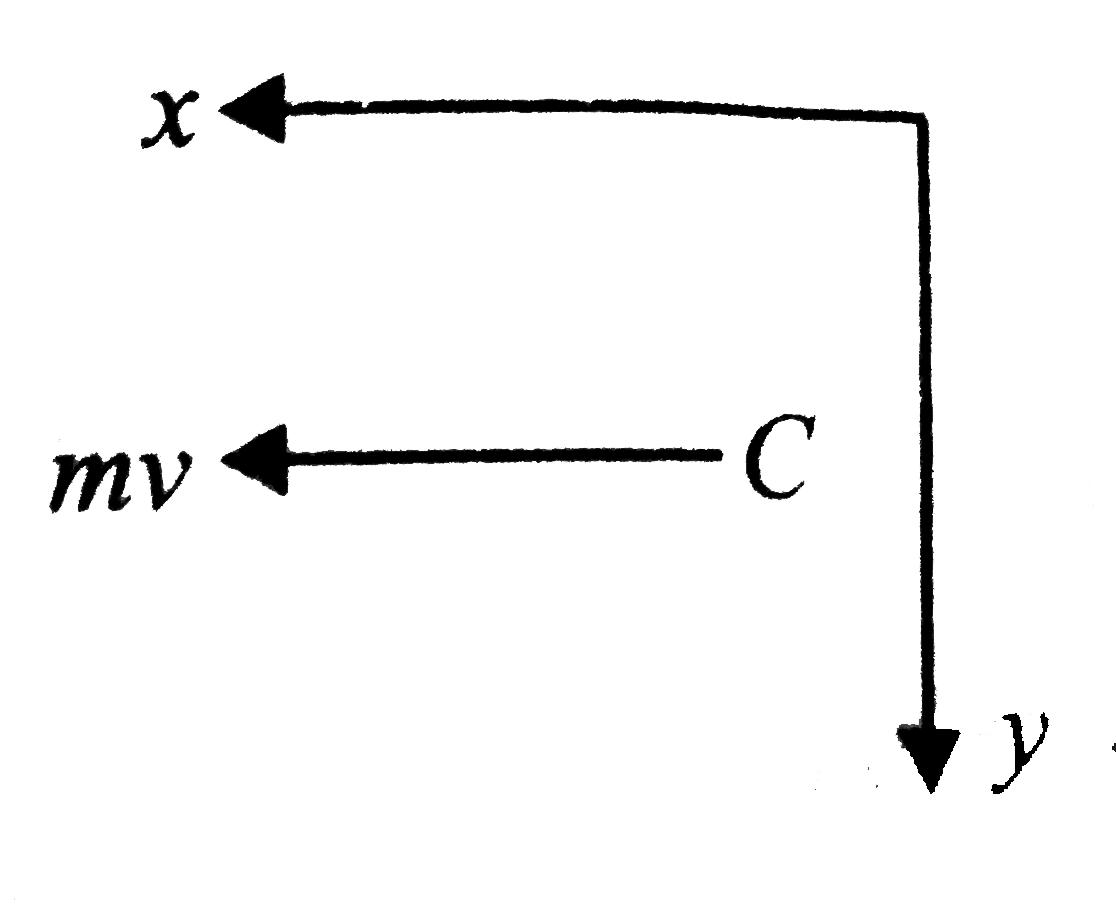
When the particle reaches point C, the momentum is as shown in figure.
(pf)x=mv..........iii
(pf)h=0..........iv
Therefore (△P)x=(pf)x−(pi)x
=mv−mvcosθ..........v
(△p)y=(pf)y−(pi)y=−mvsinθ
Magnitude of change in momentum is
√[mv(1−cosθ)]2+(mvsinθ)2=2m(√2gh)sin(θ2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A heavy block of length b and height h is placed at rest on a rough inclined plane of inclination θ with the horizontal, as shown in figure.
 View Solution
View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ - Question 2 - Select One
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1 - Question 3 - Select One or More
A particle sides down from rest on an inclined plane of angle θ with horizontal. The distances are as shown. The particle slides down to the position A, where it velocity is v.
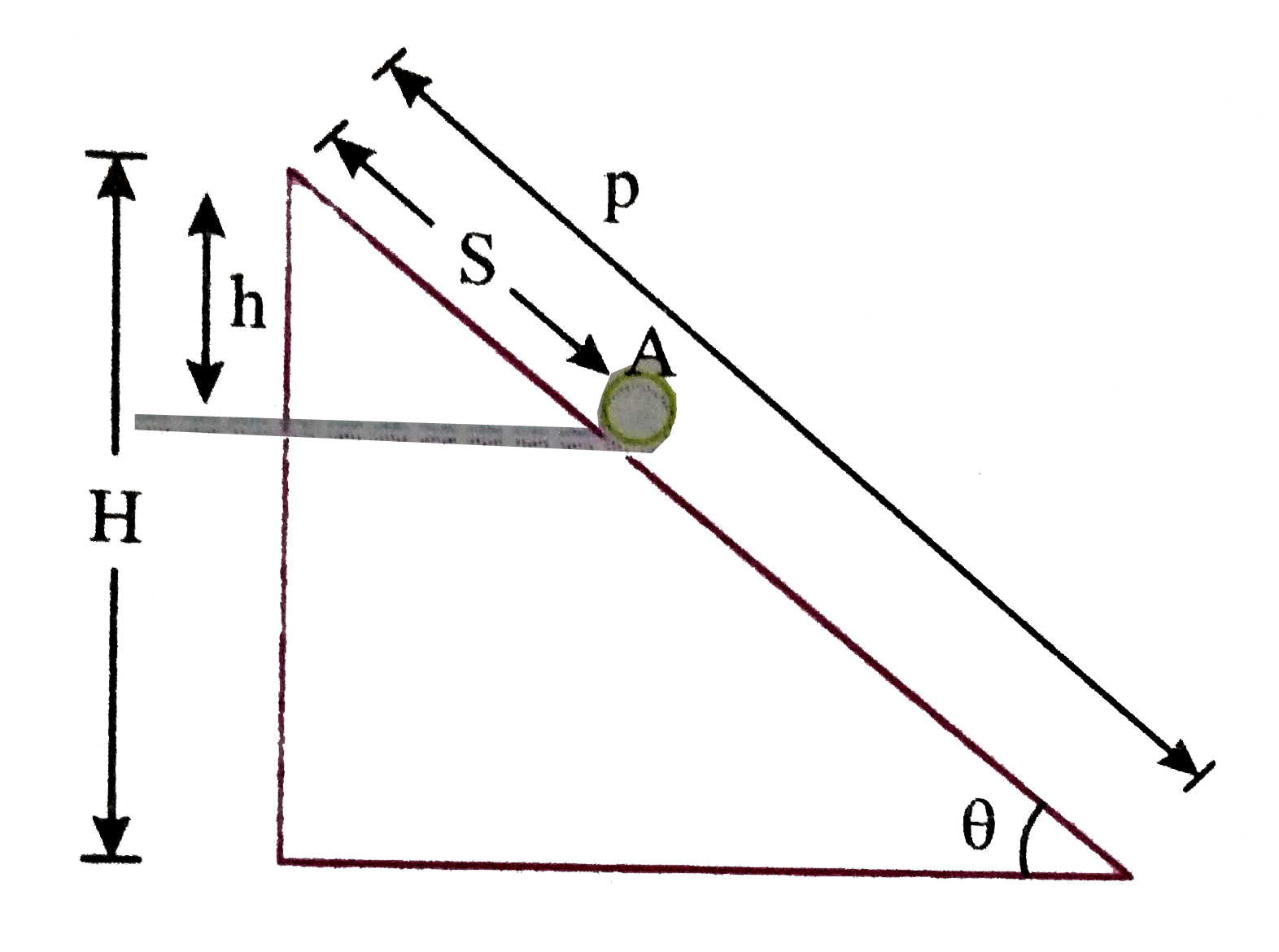 .A(v2−2gh) will remain zeroB(v2−2gssinθ) will remain zeroC[v2−2gs(H−h)(p−s)] will remain zeroD[v2−2gsHp] will remain zero.
.A(v2−2gh) will remain zeroB(v2−2gssinθ) will remain zeroC[v2−2gs(H−h)(p−s)] will remain zeroD[v2−2gsHp] will remain zero.
A trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.
 View Solution
View SolutionThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
View SolutionThe time taken by a particle to slide down a smooth inclined plane is double the time it would take in falling down through a height equal to the vertical height of the plane. The inclination of the plane with horizontal is :
View SolutionA ring of mass m and radius R is rolling down on a rough inclined plane of angle θ with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
View SolutionA brick of mass 2kg just begins to slide down on inclined plane at an angle of 45∘ with the horizontal. The force of friction will be
View Solution

