A particle of mass m is kept on a fixed , smooth sphere of radius R at a position, where the rdius thrugh the particle makes an angle of 300 with the vertical. The particle is releases from this positon. a. What is the force exerted by the sphere on teh particle just after the release? b. Find the distance travelled by the particle before it leaves contact with the sphere.
The correct Answer is:B, C, D
a. When the particle is released from rest ure the centrifugal force is zero.
N force =mgcosθ=mgcos300
=√32mg
b. When the particle leaves contact with the surface ure N=θ

So,mv2R=mgcosθ
→v2=Rcosθ ........i
Aga∈<br>(12)mv2=mgR(cos300−cosθ)
→v2=2rg(√32−cosθ)........ii
omequationiandequationii<br>Rgcostheta=2Rg[sqrt3/2-costheta]<br>rarr 3costheta=sqrt(3)<br>rarr costheta=1/sqrt3<br>or theta=cos^-1 1/sqrt3<br>so,thedistancetravelldbythepartic≤before≤av∈gcontact<br>L=R(theta-pi/6)<br>[∵30^0=(pi/6)]<br>putting the value of theta we get<br>L=0.43R
Topper's Solved these Questions
Similar Questions
A small box of mass m is kept on a fixed, smooth sphere of radius R at a position where the radius through the box makes an angle of 30∘ with the vertical. The box is released from this position
(a) What is the force exerted by the sphere on the box just after the release ?
(b) Find the distance travelled by the box before it leaves contact with the sphere.
View SolutionA particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of α with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cosα=3/4)
View Solution
Knowledge Check
A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if v<√gRBit will start moving along a circular path if v>√gRCit will start moving along a parabolic path if v<√gRDit will start moving along a parabolic path if v>√gRA particle of mass m begins to slide down on a fixed smooth sphere from the top, when it breaks off the sphere, the tangential accleration will be
A2g/3BgC√53gDg2A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
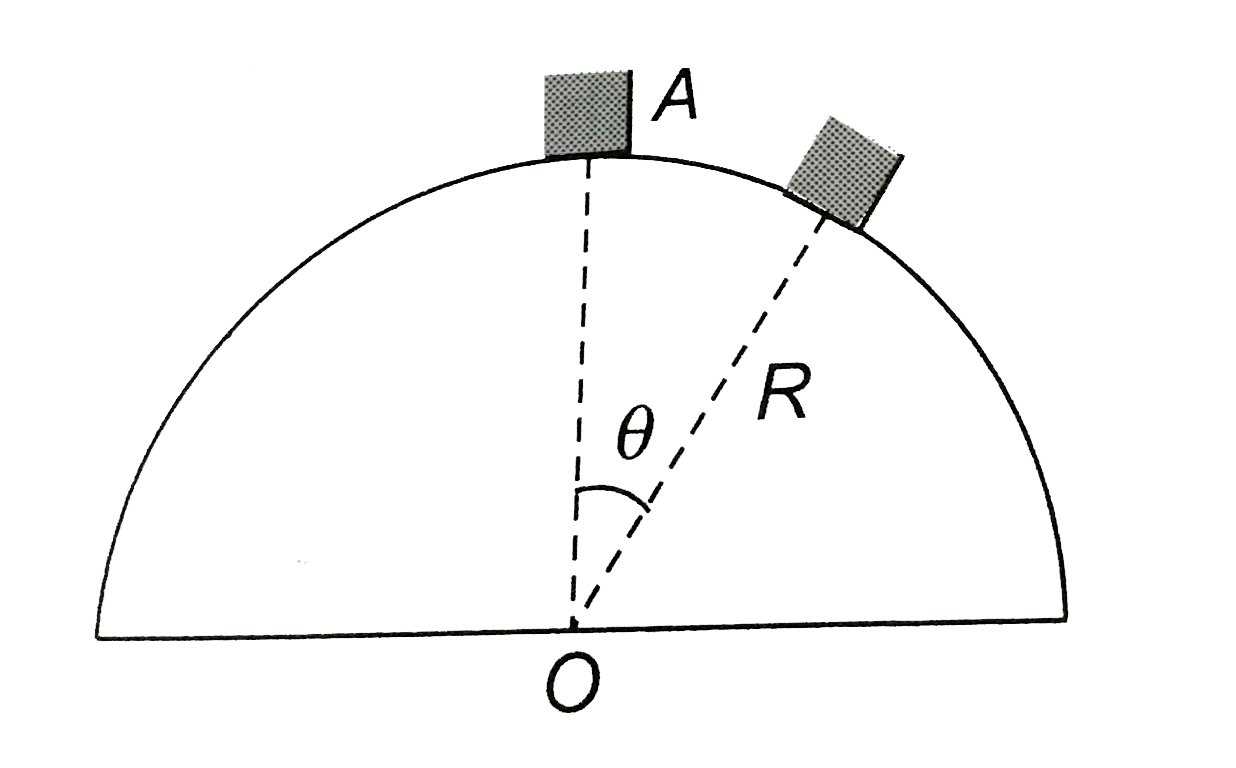 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
A small box of mass m is placed on the outer surface of a smooth fixed sphere of radius R at a point where the radius makes a angle Pse with the vertical. The box is released from this position. Find the distance travelled by the box before it leaves contact with the sphere.
View SolutionA particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View SolutionA particle of mass m being to slide down a fixed smooth sphere from the top as shown. If its acceleration when it breaks off the sphere is 2a. The value of a is :
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA particle of mass m is kept on the top of a smooth sphere of radius LR. It is given a sharp impulse whichimparts it a horizontal speed v. a. find thenormal force between the sphere and the particle just after the impulse. B. What should be the minimum value of v for which the particle does not slip on the sphere? c. Assuming the velocity v to be half the minimum calculated in part, d. find teh angle made by the radius through the particle with the vertical when it leaves the sphere.

View Solution