A particle of mass m is kept on the top of a smooth sphere of radius LR. It is given a sharp impulse whichimparts it a horizontal speed v. a. find thenormal force between the sphere and the particle just after the impulse. B. What should be the minimum value of v for which the particle does not slip on the sphere? c. Assuming the velocity v to be half the minimum calculated in part, d. find teh angle made by the radius through the particle with the vertical when it leaves the sphere.

The correct Answer is:A, B, C, D
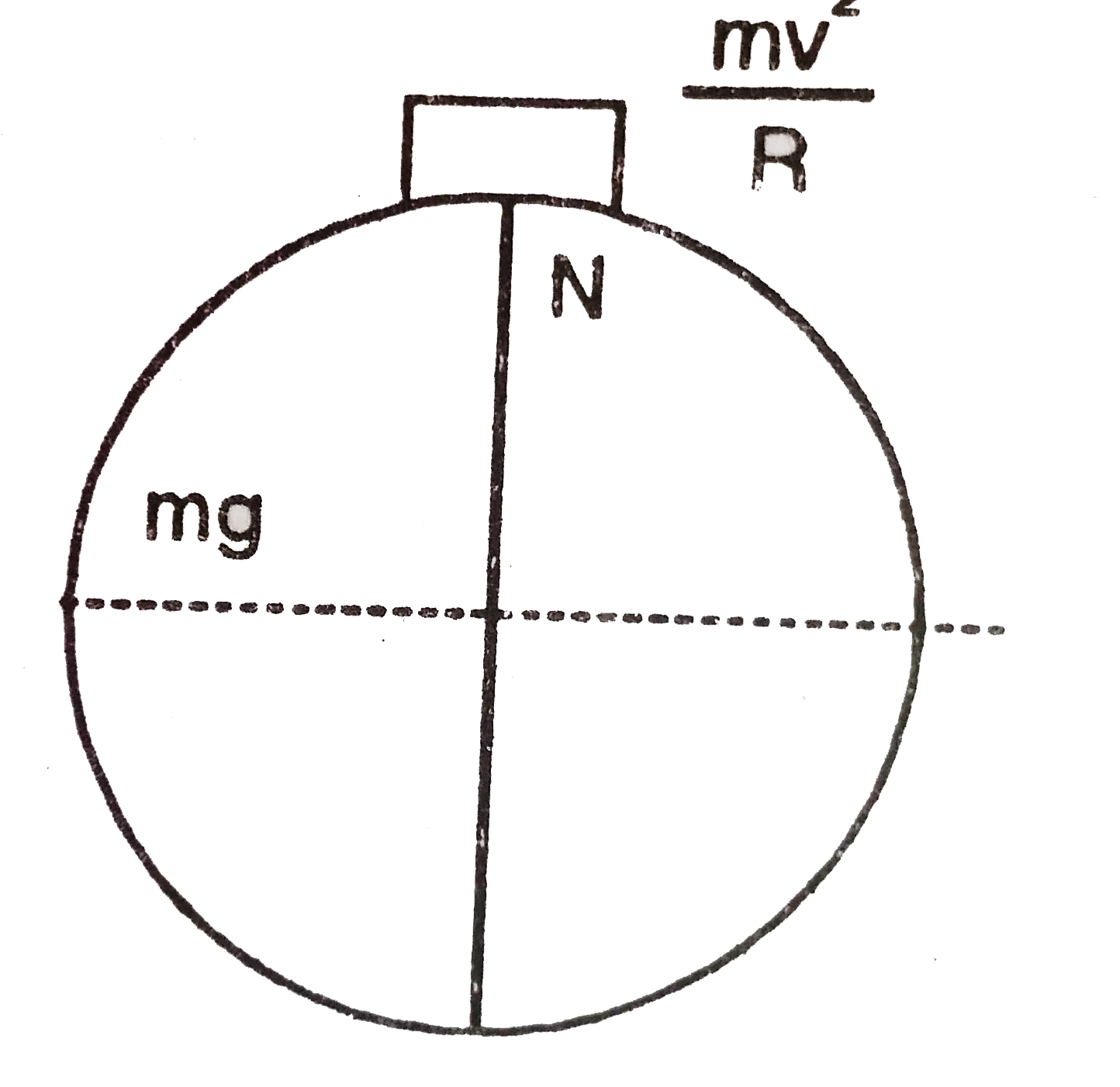
a. Radius =R
Horizontal speed=v
From the free body diagram ure
N=normal force
=mg−mv2R
 b. When the particle is givenmaximum velocity so that the centrifugal force balances the weight, the particle does not slip on the sphere,
b. When the particle is givenmaximum velocity so that the centrifugal force balances the weight, the particle does not slip on the sphere,
→mv2R=mg
→v=√gR
c if the body is given velocity v1 at the top such that
v1=√gR2
v21=gR4 Let the velocity be v2 when it leaves contact with the surface, ure

So, (mv_2^2)/R=mgcostheta<br>rarrv_2^2=Rgcostheta........i<br>Again (12)mv22−(12)mv21
=mgR(1−cosθ)
→v22=v21+2gR(1−cosθ)............ii
From equatioon i and equation ii
Rgcosθ=(Rg4)+2gR(1−cosθ)
→cosθ=(14+2−2cosθ)
→3cosθ=(94)
→θ=cos−1(34)
Topper's Solved these Questions
Similar Questions
A particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionA particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View Solution
Knowledge Check
A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if v<√gRBit will start moving along a circular path if v>√gRCit will start moving along a parabolic path if v<√gRDit will start moving along a parabolic path if v>√gRA particle of mass m is moving with a uniform velocity v1. It is given an impulse such that its velocity becomes v2. The impulse is equal to
Am(v1+v2)Bm[|v2|−|v1|]C12(v22−v21)Dm(v2−v1)A particle of mass m is moving with a uniform velocity v1. It is given an impulse such that its velocity becomes v2. The impulse is equal to
Am[|v2|−|v1|]B12m(v22−v21)Cm(v1+v2)Dm(v2−v1)
A particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.

View SolutionA particle of mass m is kept on a fixed , smooth sphere of radius R at a position, where the rdius thrugh the particle makes an angle of 300 with the vertical. The particle is releases from this positon. a. What is the force exerted by the sphere on teh particle just after the release? b. Find the distance travelled by the particle before it leaves contact with the sphere.
View SolutionA particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
View SolutionConsider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
What is the normal reaction between block and the sphere just after the impulse is applied ?
View Solution
