A particle of mass m is moving perpendicular to a rod of length L kept on a frictionless horizontal surface and collides at a distance L/4 from the centre of rod. Particle comes to state of rest just after collision. Mass of rod is M and speed of particle before collision is u. Let v is the velocity of centre of rod after collision and is angular velocity attained by the rod. Find Lωv
The correct Answer is:3
Situation described in the question is as shown in figure before and just after the collision.
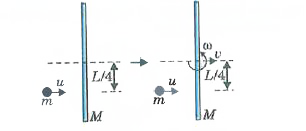
First we can apply conservation of linear momentum in the direction of initial motion of particle.
mu=Mv⇒v=muM ......(i)
We can now apply conservation of angular momentum about the centre of rod.
L1=L2
⇒muL4=ML212ω⇒Lω=3muM ......(ii)
From equations (i) and (ii) we can write the following:
Lωv=3
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)16videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )1videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Rod particle collisions and Angular Impulse
View SolutionA smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
A1BmMCM−mM+mDmM+m - Question 2 - Select One
A thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
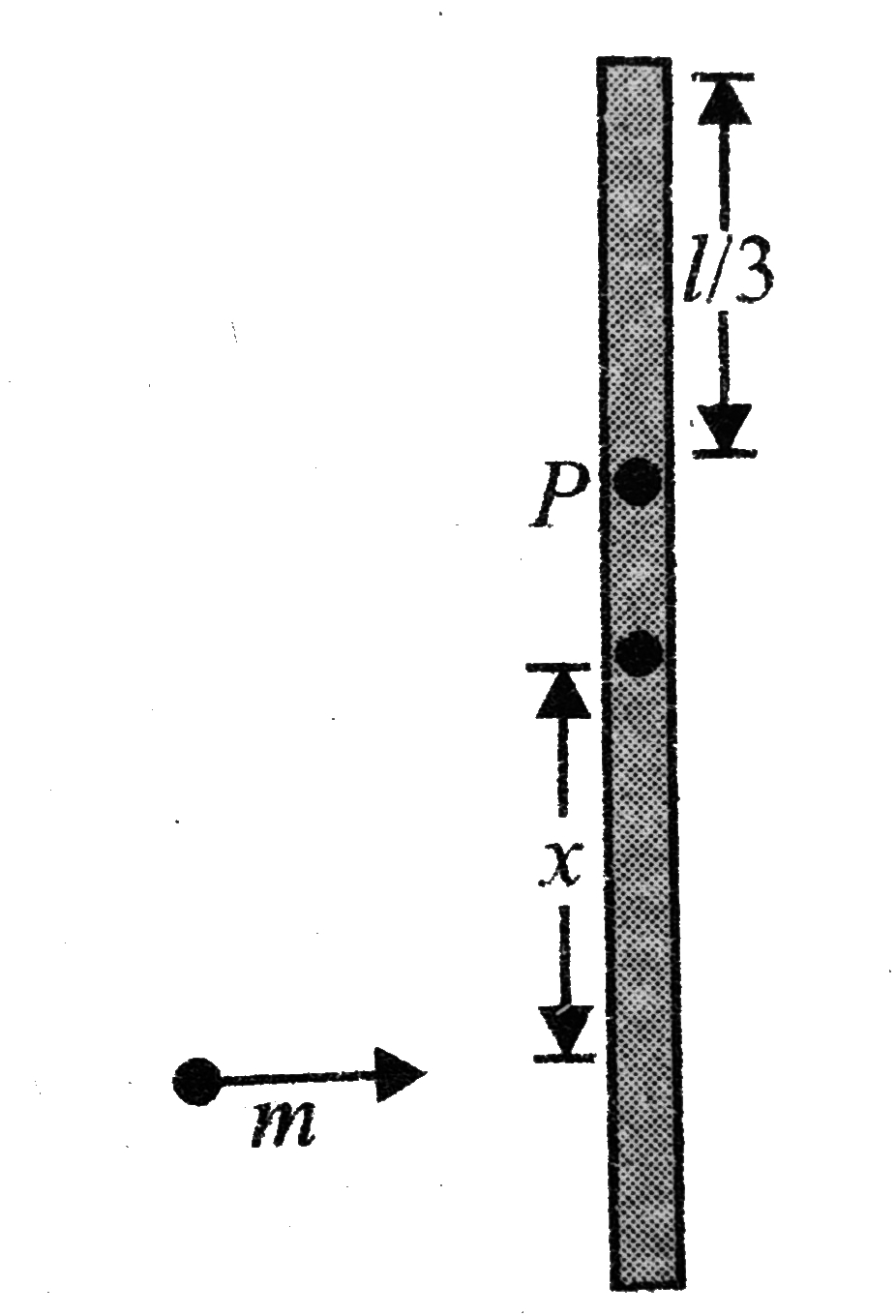 A1/2B1/3C1/6D1/4
A1/2B1/3C1/6D1/4 - Question 3 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionAMvM+mBmvM+mC2mvM+mD2MvM+m
A rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionTwo particles of mass 2kg and 6kg are moving on smooth horizontal surface collides with each other.If velocity of their common centre of mass is 10m/s before collision then what will be the total linear momentum of system of particles after collision.(Assume they move along the surface after collision)
View Solution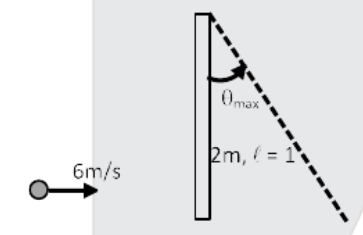
Find maximum angular displacement of rod. if particle sticks after collision.View Solution

