A particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
2Fm
F2m
2Fm
2F2m
The correct Answer is:D
To solve the problem step by step, we will use the concepts of force, acceleration, velocity, and power.
Step 1: Identify the Given Information
- Mass of the particle: m
- Force acting on the particle: F
- Time during which the force acts: t=2 seconds
- Initial velocity of the particle: u=0 (since it starts from rest)
Step 2: Calculate the Acceleration
According to Newton's second law of motion, the acceleration a can be calculated using the formula:
a=Fm
Step 3: Calculate the Final Velocity
The final velocity v of the particle after time t can be calculated using the equation of motion:
v=u+at
Substituting the values, we get:
v=0+(Fm)⋅2=2Fm
Step 4: Calculate the Power
Power P is defined as the work done per unit time. The work done W by the force is given by:
W=F⋅s
where s is the displacement. The displacement can be calculated using the equation:
s=ut+12at2
Substituting the values:
s=0+12⋅(Fm)⋅(22)=12⋅(Fm)⋅4=2Fm
Now, substituting s into the work done equation:
W=F⋅2Fm=2F2m
Step 5: Calculate the Average Power
The average power P over the time interval t is given by:
P=Wt=2F2m2=F2m
Step 6: Determine Maximum Power
The maximum power attained by the particle when the force is applied for the full duration of 2 seconds is:
Pmax=F2m
Final Answer
Thus, the maximum power attained is:
F2m
---
- Mass of the particle: m
- Force acting on the particle: F
- Time during which the force acts: t=2 seconds
- Initial velocity of the particle: u=0 (since it starts from rest)
According to Newton's second law of motion, the acceleration a can be calculated using the formula:
a=Fm
The final velocity v of the particle after time t can be calculated using the equation of motion:
v=u+at
Substituting the values, we get:
v=0+(Fm)⋅2=2Fm
Power P is defined as the work done per unit time. The work done W by the force is given by:
W=F⋅s
where s is the displacement. The displacement can be calculated using the equation:
s=ut+12at2
Substituting the values:
s=0+12⋅(Fm)⋅(22)=12⋅(Fm)⋅4=2Fm
W=F⋅2Fm=2F2m
The average power P over the time interval t is given by:
P=Wt=2F2m2=F2m
The maximum power attained by the particle when the force is applied for the full duration of 2 seconds is:
Pmax=F2m
Thus, the maximum power attained is:
F2m
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
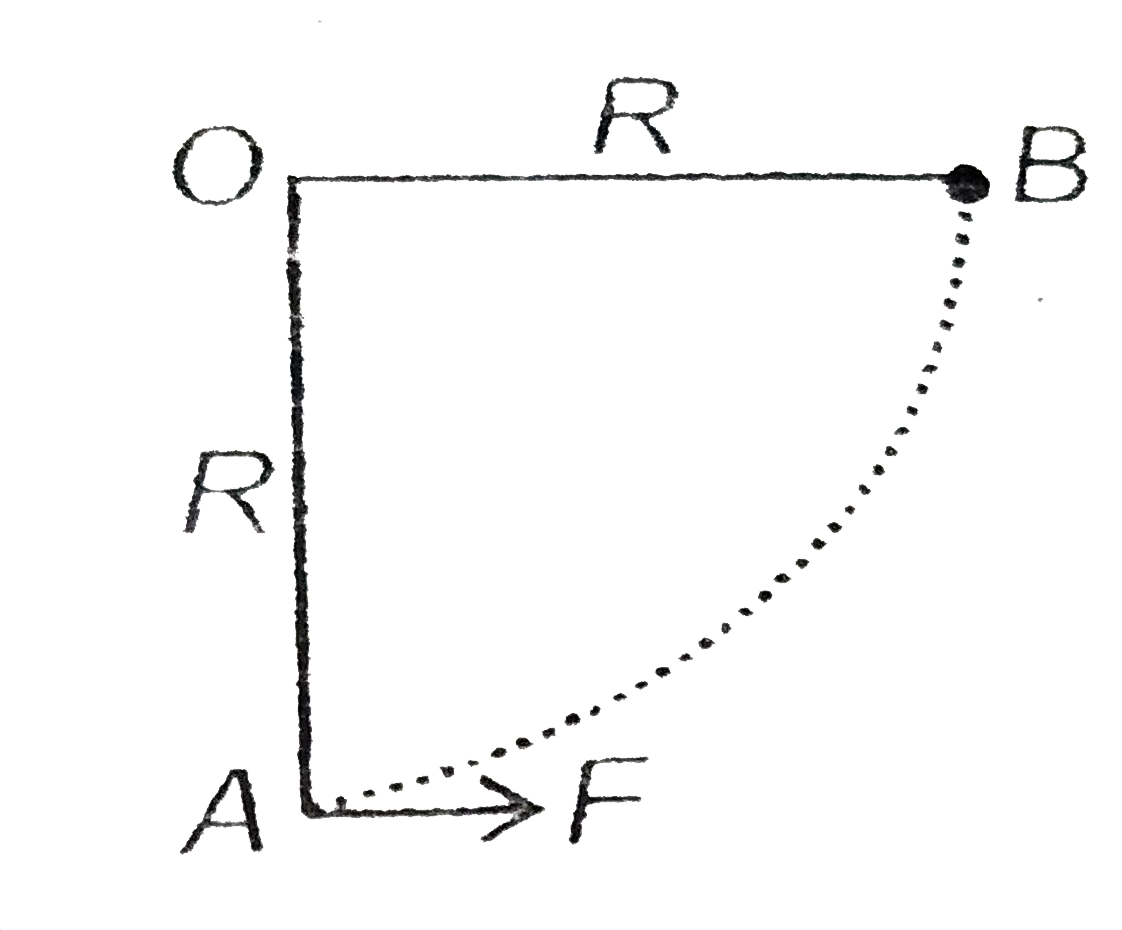
A block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
View SolutionAn object of mass m, initially at rest under the action of a constant force F attains a velocity v in time t. Then, the average power supplied to mass is
View SolutionUnder the action of a constant force, A particle is experiencing a constant acceleration. The power is
View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
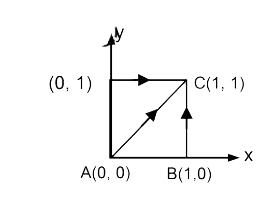
View Solution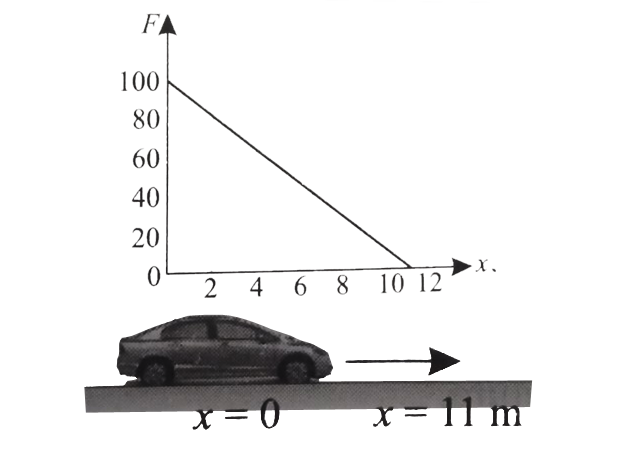
A toy car of mass 5 kg moves up a ramp under the influence of force F plotted against displacement x. The maximum height attained is given by
View SolutionA particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
View SolutionA particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
View SolutionA particle start moving from rest state along a straight line under the action of a constant force and travel distance x in first 5 seconds. The distance travelled by it in next five seconds will be
View SolutionA particle of mass 2kg moves in the xy plane under the action of a constant force →F where →F=ˆi−ˆj. Initially the velocity of the particle is 2ˆj. The velocity of the particle at time t is
View SolutionThe KE acquired by a mass m in travelling a certain distance s, starting from rest, under the action of a constant force is directly proportional to :
View Solution
