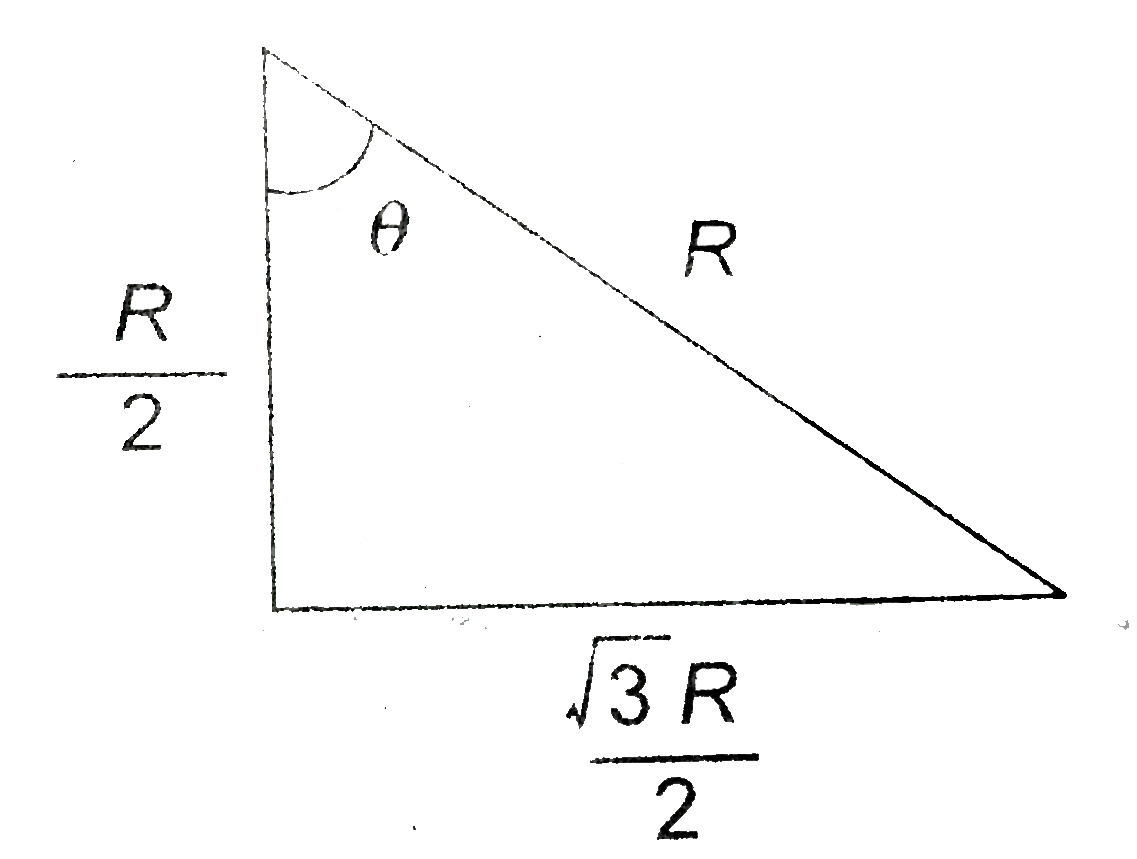
A particle of mass moving with velocity collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

The particle and sphere will perpendicular after the collision.
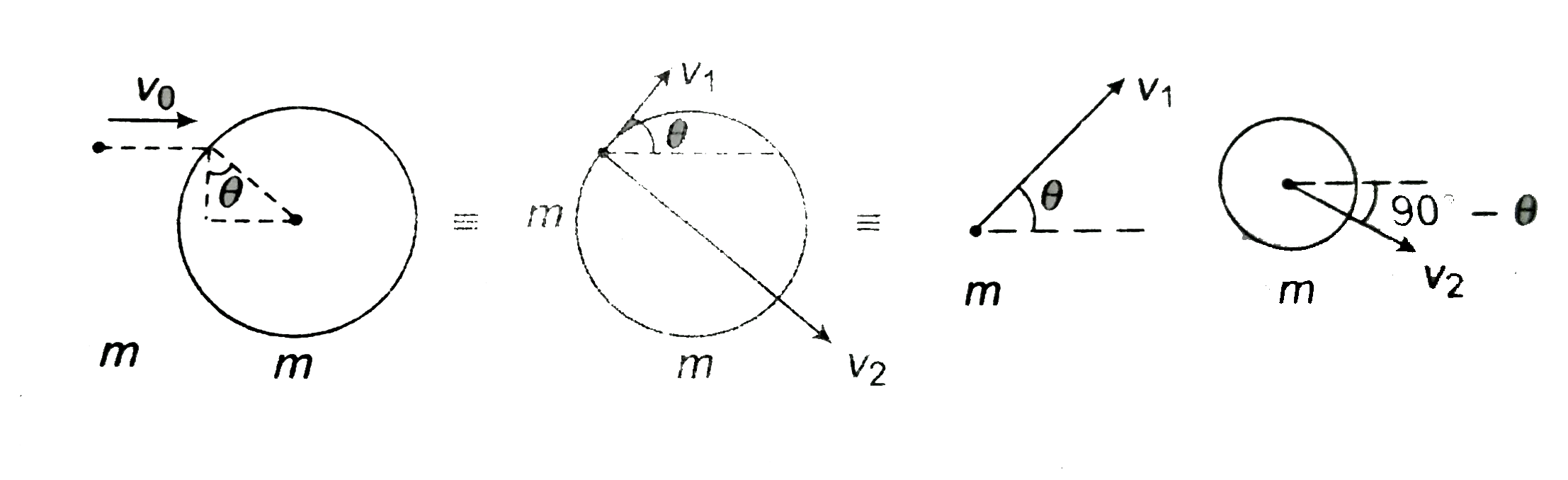
By the momentum conservation:
x-ax is:
(i)
Solving (i) and (ii),

Topper's Solved these Questions
Similar Questions
A particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
View SolutionA particle of mass m moving on a smooth surface with velocity 10m/s strikes another particle of mass 2m moving with 5m/s in the same direction . If the collision is elastic and head - on , find velocities of particles after the collision.
View Solution
Knowledge Check
A particle of mass m1 moving with velocity v collides with a mass m2 at rest, then they get embedded. Just after collision, velocity of the system
AincreasesBdecreasesCremains constantDbecomes zeroA sphere of mass 'm' moving with velocity 'v' collides head-on on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is (e is coefficient of restitution and collision is inelastic)
Ae−12Be2Ce+12DeA particle of mass m moving with velocity →V makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
A→VB−→VC−2→VDzero
A particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View SolutionA particle of mass m moving with velocity 2v collides with another particle of mass 3m moving with velocity v in the same direction.If it is perfect inelastic collision,the loss of kinetic energy of the system is
View SolutionA small particle of mass m is released from a height h on a large smooth sphere kept on a perfectly smooth surface as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.
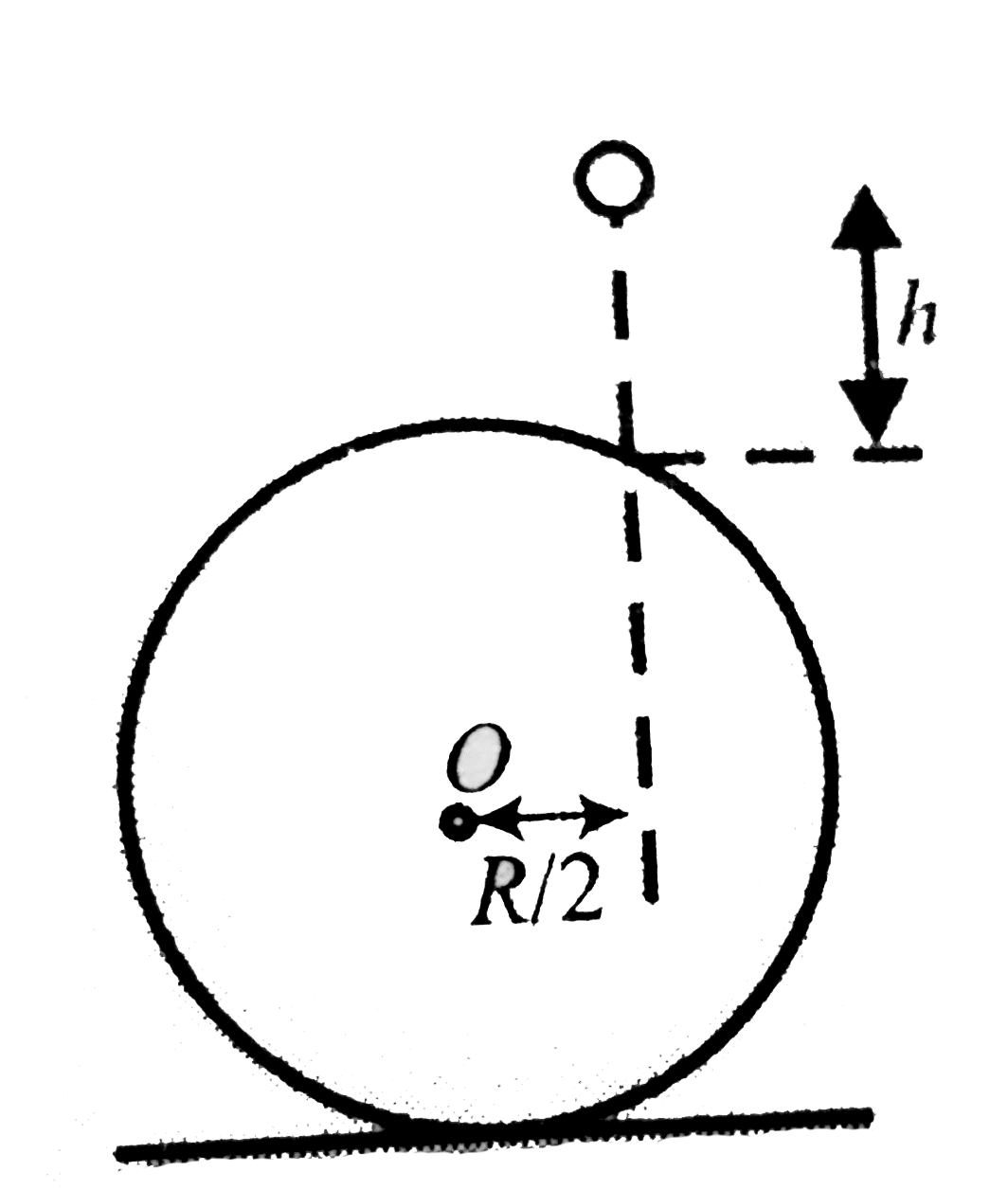
View SolutionA small particle of mass m is released from a height h on a large smooth sphere kept on a perfectly smooth surface as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.

View Solution
