A particle oscillates between the points x=40mm and x=160mm with an acceleration a =k(100-x),where k is a constant.The velocity of the particle is 8 m m/s when =100 mm and is zero at both x=40 mm and x=160mm.Determine (a)the value of k (b) the velocity when x=120 mm.
To solve the problem, we need to determine the value of the constant k and the velocity of the particle when it is at x=120mm.
1. Understanding the Given Information:
- The particle oscillates between x=40mm and x=160mm.
- The acceleration is given by a=k(100−x).
- The velocity is 8mm/s when x=100mm.
- The velocity is 0mm/s at both x=40mm and x=160mm.
2. Using the Relationship Between Acceleration and Velocity:
- We know that acceleration a can be expressed as a=vdvdx.
- Therefore, we can write:
vdvdx=k(100−x)
3. Separating Variables and Integrating:
- Rearranging gives:
vdv=k(100−x)dx
- Integrating both sides:
∫vdv=∫k(100−x)dx
- This results in:
v22=k(100x−x22)+C
4. Finding the Constant C:
- We know that when x=40mm, v=0:
0=k(100⋅40−4022)+C
- Calculating:
0=k(4000−800)+C⇒C=−k⋅3200
5. Substituting Back to Find k:
- Now substituting C back into our equation:
v22=k(100x−x22)−k⋅3200
- When x=100mm, v=8mm/s:
822=k(100⋅100−10022)−k⋅3200
- Simplifying:
32=k(10000−5000)−k⋅3200
32=k⋅5000−k⋅3200
32=k⋅1800
- Thus, we find:
k=321800=16900≈0.01778
6. Finding the Velocity at x=120mm:
- Now we substitute k and x=120 into the equation:
v22=k(100⋅120−12022)−k⋅3200
- Substituting k:
v22=321800(12000−7200)−321800⋅3200
- Simplifying:
v22=321800⋅4800−321800⋅3200
v22=321800⋅(4800−3200)=321800⋅1600
v22=32⋅16001800=512001800≈28.44
- Therefore:
v2=2⋅28.44≈56.88
v≈√56.88≈7.53mm/s
Final Answers:
(a) The value of k is approximately 0.01778mm−1.
(b) The velocity when x=120mm is approximately 7.53mm/s.
- The particle oscillates between x=40mm and x=160mm.
- The acceleration is given by a=k(100−x).
- The velocity is 8mm/s when x=100mm.
- The velocity is 0mm/s at both x=40mm and x=160mm.
- We know that acceleration a can be expressed as a=vdvdx.
- Therefore, we can write:
vdvdx=k(100−x)
- Rearranging gives:
vdv=k(100−x)dx
- Integrating both sides:
∫vdv=∫k(100−x)dx
- This results in:
v22=k(100x−x22)+C
- We know that when x=40mm, v=0:
0=k(100⋅40−4022)+C
- Calculating:
0=k(4000−800)+C⇒C=−k⋅3200
- Now substituting C back into our equation:
v22=k(100x−x22)−k⋅3200
- When x=100mm, v=8mm/s:
822=k(100⋅100−10022)−k⋅3200
- Simplifying:
32=k(10000−5000)−k⋅3200
32=k⋅5000−k⋅3200
32=k⋅1800
- Thus, we find:
k=321800=16900≈0.01778
- Now we substitute k and x=120 into the equation:
v22=k(100⋅120−12022)−k⋅3200
- Substituting k:
v22=321800(12000−7200)−321800⋅3200
- Simplifying:
v22=321800⋅4800−321800⋅3200
v22=321800⋅(4800−3200)=321800⋅1600
v22=32⋅16001800=512001800≈28.44
- Therefore:
v2=2⋅28.44≈56.88
v≈√56.88≈7.53mm/s
(a) The value of k is approximately 0.01778mm−1.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Question for descriptiv Answers
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Short answer type question
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
If v=x2−5x+4, find the acceleration of the particle when velocity of the particle is zero.
View SolutionA particle moves along the positive x-axis with an accelerationax which increases linearly with x, as shown in the graph. If the velocity of the particle at x=4cm is 0.40m/s determine the velocity at x=12cm
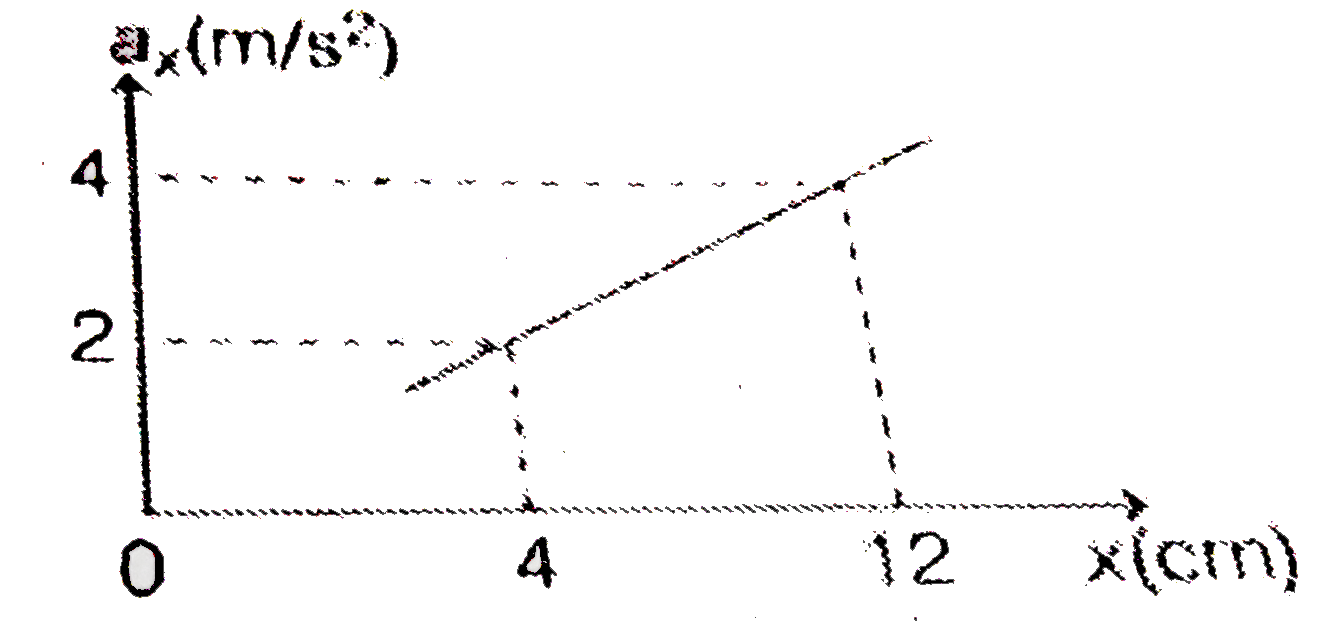
View Solution
Knowledge Check
If y=kx, where k is a constant, and y=24 when x=6, what is the value of y when x=5 ?
A6B15C20D23
If y=kx, where k is a constant and y=27 when x=18, what is the value of y when x=30?
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View SolutionIf xy=k, where k is a constant and y=21, when x=6, what is the value of y when x=9?
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionA particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time t=0 and is zero when t=10s. If the velocity of the particle is momentary zero when t=6s, determine the acceleration a and the velocity v when t=10s.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
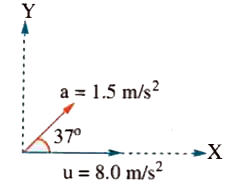
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionReferring to a−x graph, find the velocity when thedisplacement of the particle is 100m. Assume intial velocity as zero.
 .
.
View Solution
