A particle projected atv a definite angle ∝ to the horizontal passes through points (a,b)and(b,a), referred to horizontal and vertical axes through the points of projection. Show that :
(a) The horizontal range R=a2+ab+b2a+b .
(b) The angle of projection ∝ is given by
tan−1[a2+ab+b2ab].
(a) The equation of the trajectory of the particle
y=xtan∝(1−xR)….(i)
Since the particle passes through the points with coordinates (a,b)and(b,a), they should satisfy the equation of the curve.
b=atan∝(1−aR)and(ii)a=btan∝(1−bR) ...(ii)
Dividing b2a2=(1−aR)(1−bR)
⇒b2−b3R=a2−a3R
⇒1R[a3−b3]=a2−b2
⇒R=a3−b3a2−b2=(a−b)(a2+ab+b2)(a−b)(a+b)=a2+ab+b2a+b
Hence, proved. [∴a≠b]
(b) Substituting the expression for R in (ii),
ba=tan∝[1−a(+b)a2+ab+b2]
=tan∝[a2+ab+b2−a2−aba2+ab+b2]
tan∝=a2+ab+b2ab⇒∝=tan−1[a2+ab+b2ab]
Hence proved.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle is projected at an angle of tan−1(43) with horizontal from a point O.The ratio of the range on the horizontal plane through O to the maximum height ascended above O is
View SolutionA body is projected at an angle θ with the horizontal. Derive an expression for its horizontal range. Show that there are two angles θ1 and θ2 projections for the same horizontal range, such that θ1+θ2=90∘.
View Solution
Knowledge Check
A particle is projected with an angle of projection θ to the horizontal line passing through the points (P,Q) and (Q,P) referred to horizontal and vertical axes (can be treated as X-axis and Y-axis respectively). The angle of projection can be given by
Atan−1[P2+PQ+Q2PQ]Btan−1[P2+Q2−PQPQ]Ctan−1[P2+Q22PQ]Dsin−1[P2+Q2+PQ2PQ]A ball is projected at an angle 45∘ with horizontal. It passes through a wall of height h at horizontal distance d1 from the point of projection and strikes the ground at a horizontal distance (d1+d2) from the point of projection, then
Ah=2dd_(2)d+d2Bh=d1d2d1+d2Ch=√2d1d2d1+d2Dh=d1d22(d1+d2)A particle is projected with speed 30m/s at angle 22.5∘ with horizontal from ground as shown. AB and CD are parallel to y-axis and B is highest point of trajectory of particle. CD/AB is
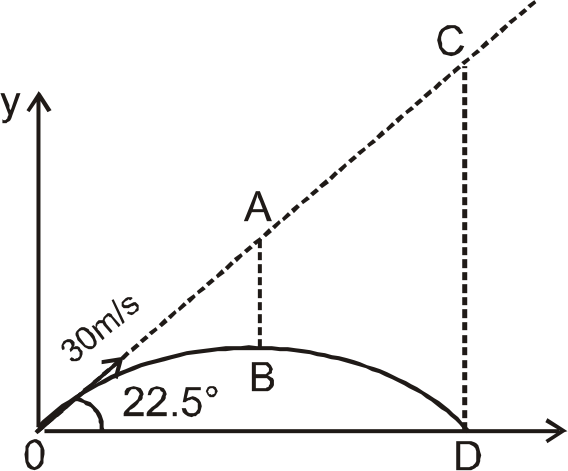 A3B3/2C2D4
A3B3/2C2D4
If the horizontal range of a projectile be a and the maximum height attained by it is b, then prove that the velocity of projection is
View SolutionA particle is projected from origin at an angle is selected as X-axis and verticle as Y-axis . It is found that particle passes through the points (a, b) and (b, a). Calculate range and angle of projection .
View SolutionA particle is projected at an angle ∝ with horizontal from the foot of a plane whose inclination to β Show that it will strike the plane at right angles if cotβ=2tan(∝−β)
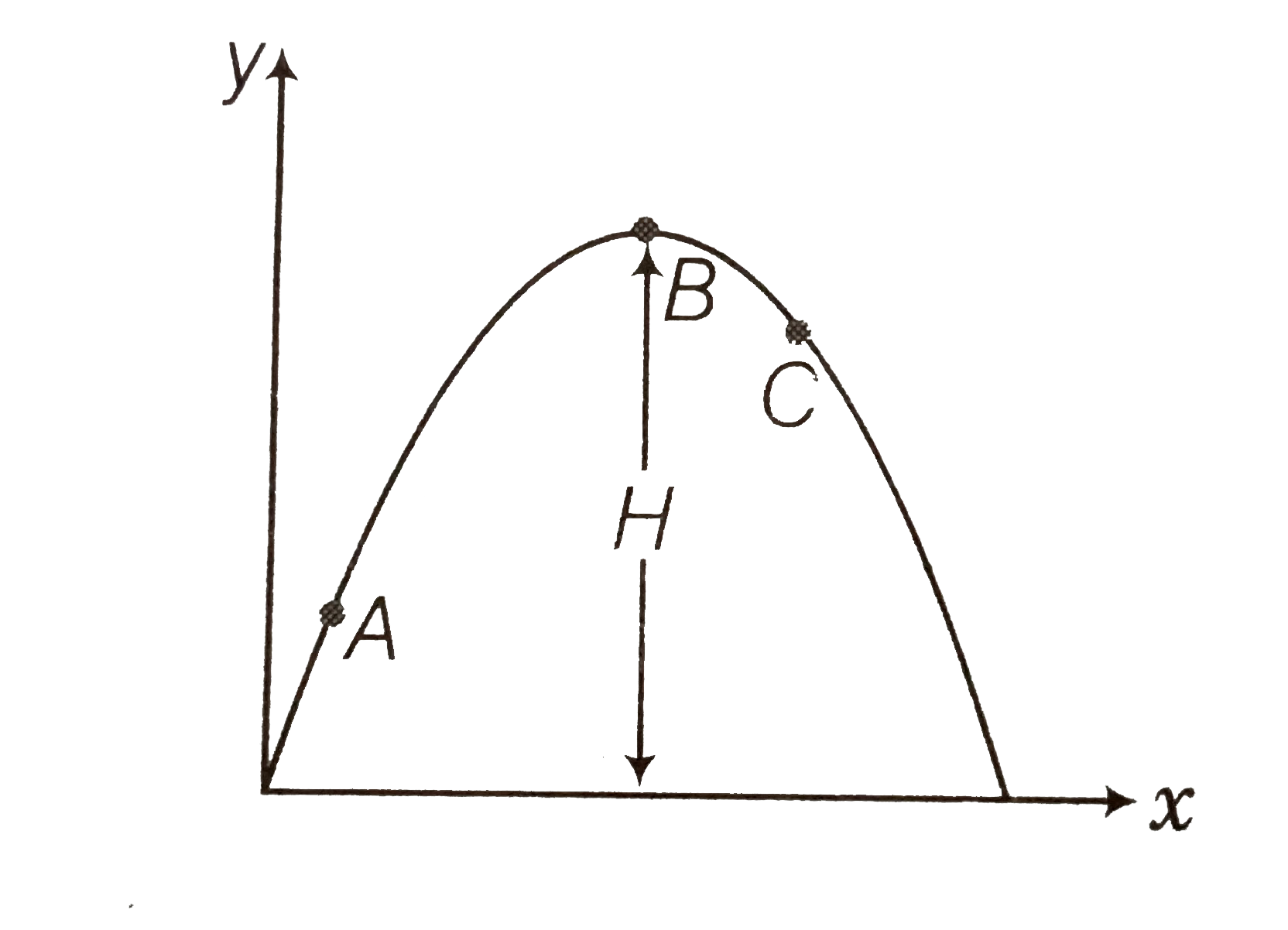
View SolutionA particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure where x and y indicate horizontal and vertical directions, respectively . Shown in the diagram, direction of velocity and acceleration at points A, B and C.
View SolutionA line passes through the points A(2,-1,1) and B(1,2-2) .The equations of the lines AB are
View Solution
