A particle slides down a frictionless paraboli (y=x2) track (A−B−C) starting from rest at point A.Point B is at the vertex of parabola and point C is at a height less than that of point A.After C,the particle moves freely in air as a projectile. If the particle reaches highest point at P,then
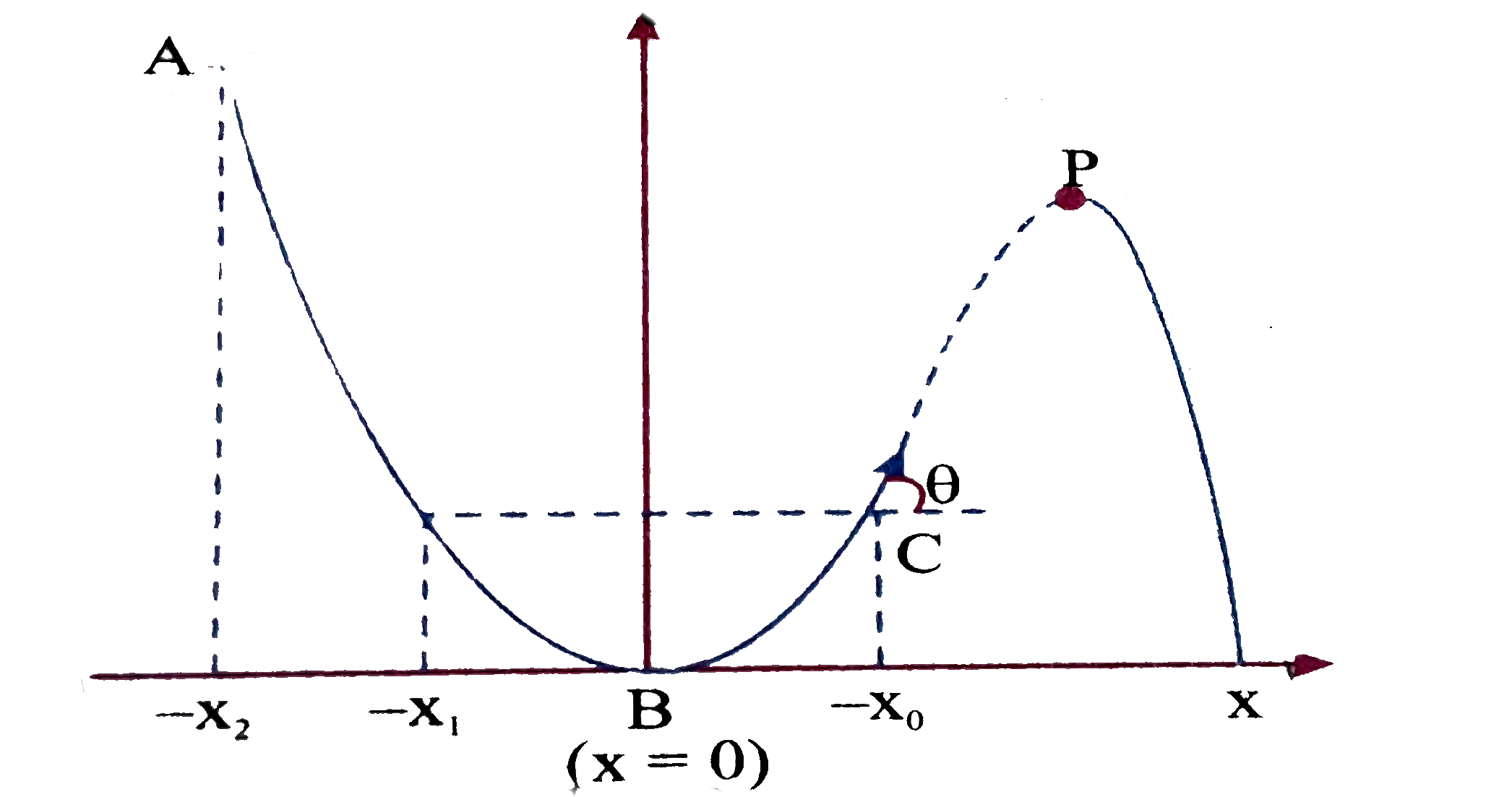
(a) KE at P=KEatB
(b) height at P = height at (A)
(c ) total eneragy at P=→tale≠ragyat(A)
(d) time of travel from A oto B = time of travel from (B) tp (P).
The correct Answer is:C
Since y=x2 , the motion is in two dimensions as shown in figure. Velocity at (B) greater than at (P) . In the given motion of a particle, the law of conservation of energy . Therefore, total energy at P= total eneragy at (A). As vertical distance AB>BP, time of travel from (A) to (B) is greater than that from (B) to (P).
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 NCERT multiple161videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 NCERT multiple Choice10videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT multiple11videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
A particle (m = 3 kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaching its highest point P (height 1.5 m) the kinetic energy of the prarticle (in J) is : Figure drawn is schematic and not to scale , take g = 10ms−2
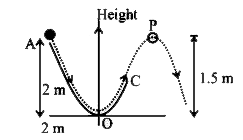 View Solution
View SolutionA particle (m = 2 kg) slides down a smooth track AOC starting from rest at point A (height = 5m). After reaching point C (height =1m), the particle continues to move freely in air as a projectile. The particle velocity at point C is at angle 60∘ with the horizontal. The maximum height attained by particle after leaving point C is _____(in m). [figure drawn is schematic and hot to scale : take =ms−2]
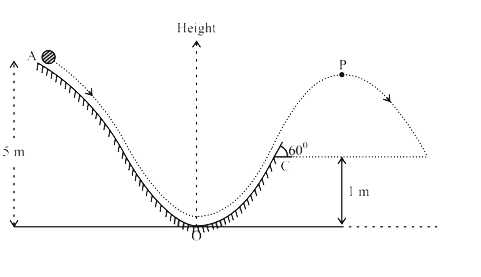 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m slides on a frictionaless surface ABCD, starting from rest as shown in figure. The part BCD is a circular arc. If it looses contact at point P, the maximum height attained by the particle from point C is
 A(a) R[2+12√2]B(b) R[1+12√2]RC(c) 3RD(d) None of these
A(a) R[2+12√2]B(b) R[1+12√2]RC(c) 3RD(d) None of these - Question 2 - Select One
Velocity of a particle varies with time as v=atˆi+2ht2ˆj. If the particle starts from point (0,c), the trajectory of the particle is
Ay=bx3/2a+cBy=4√2b3(xa)3/2+cCy=4√2b3(xa)3/2−cDy=bx3/2a−c - Question 3 - Select One
A particle is dropped from height H. At a point its kinetic energy is x times of its potential energy. Find the speed of the particle at that point -
A[2gxH]1/2B[2g(x+1)Hx]1/2C[2gH(x+1)]1/2D[2gxH(x+1)]1/2
A particle (m = 1kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaches point C (height 1 m), the vertical speed of the particle (in m/s) is (Figure drawn is schematic and not to scale , take g = 9.8 m/sec2) [Take ]
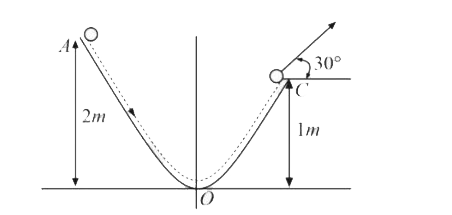 View Solution
View SolutionIn the illustration 1 if the particle shifts from Points P to points C find the displacement of the particle.
View Solution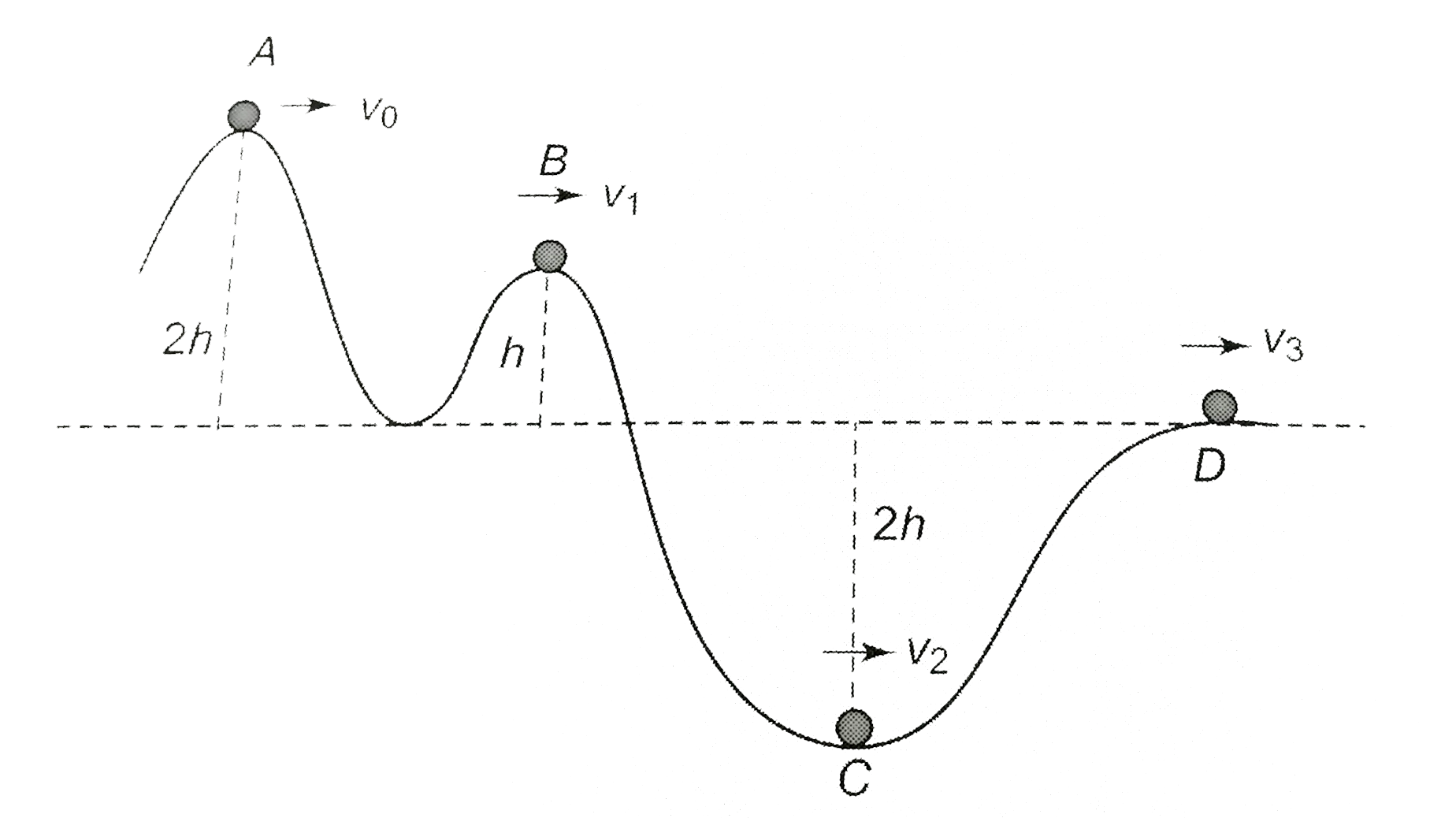
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and DView SolutionNormal to the parabola y2=8x at the point P (2, 4) meets the parabola again at the point Q. If C is the centre of the circle described on PQ as diameter then the coordinates of the image of point C in the line y=x are
View SolutionA particle starts from point A moves along a straight line path with an acceleration given by a=p−qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
View Solution

