A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of displacement (a) in successive second and (b) in successive time interval t0.
To solve the problem, we need to find the displacement of a particle moving under constant acceleration in two different scenarios: (a) in successive seconds and (b) in successive time intervals.
Part (a): Displacement in Successive Seconds
1. Understanding the Formula:
The displacement sn in the nth second can be calculated using the formula:
sn=u+12a(2n−1)
where u is the initial velocity, a is the acceleration, and n is the second for which we want to find the displacement.
2. Initial Conditions:
Since the particle starts from rest, we have:
u=0
Therefore, the formula simplifies to:
sn=12a(2n−1)
3. Calculating Displacements:
- For the 1st second (n=1):
s1=12a(2⋅1−1)=12a(1)=a2
- For the 2nd second (n=2):
s2=12a(2⋅2−1)=12a(3)=3a2
- For the 3rd second (n=3):
s3=12a(2⋅3−1)=12a(5)=5a2
4. Finding the Ratio:
The displacements in successive seconds are:
- s1=a2
- s2=3a2
- s3=5a2
The ratio of displacements in successive seconds is:
s1:s2:s3=a2:3a2:5a2=1:3:5
Part (b): Displacement in Successive Time Intervals
1. Understanding the Formula:
The displacement Sn from time 0 to t can be calculated using:
Sn=ut+12at2
Again, since the particle starts from rest, u=0:
Sn=12at2
2. Calculating Displacements:
- For t=1:
S1=12a(12)=a2
- For t=2:
S2=12a(22)=12a(4)=2a
- For t=3:
S3=12a(32)=12a(9)=9a2
3. Finding the Ratio:
The displacements in successive time intervals are:
- S1=a2
- S2=2a
- S3=9a2
The ratio of displacements is:
S1:S2:S3=a2:2a:9a2=1:4:9
Final Answers:
- (a) The ratio of displacement in successive seconds is 1:3:5.
- (b) The ratio of displacement in successive time intervals is 1:4:9.
The displacement sn in the nth second can be calculated using the formula:
sn=u+12a(2n−1)
where u is the initial velocity, a is the acceleration, and n is the second for which we want to find the displacement.
Since the particle starts from rest, we have:
u=0
Therefore, the formula simplifies to:
sn=12a(2n−1)
- For the 1st second (n=1):
s1=12a(2⋅1−1)=12a(1)=a2
- For the 2nd second (n=2):
s2=12a(2⋅2−1)=12a(3)=3a2
- For the 3rd second (n=3):
s3=12a(2⋅3−1)=12a(5)=5a2
The displacements in successive seconds are:
- s1=a2
- s2=3a2
- s3=5a2
s1:s2:s3=a2:3a2:5a2=1:3:5
The displacement Sn from time 0 to t can be calculated using:
Sn=ut+12at2
Again, since the particle starts from rest, u=0:
Sn=12at2
- For t=1:
S1=12a(12)=a2
- For t=2:
S2=12a(22)=12a(4)=2a
- For t=3:
S3=12a(32)=12a(9)=9a2
The displacements in successive time intervals are:
- S1=a2
- S2=2a
- S3=9a2
S1:S2:S3=a2:2a:9a2=1:4:9
- (a) The ratio of displacement in successive seconds is 1:3:5.
- (b) The ratio of displacement in successive time intervals is 1:4:9.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.110videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.210videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
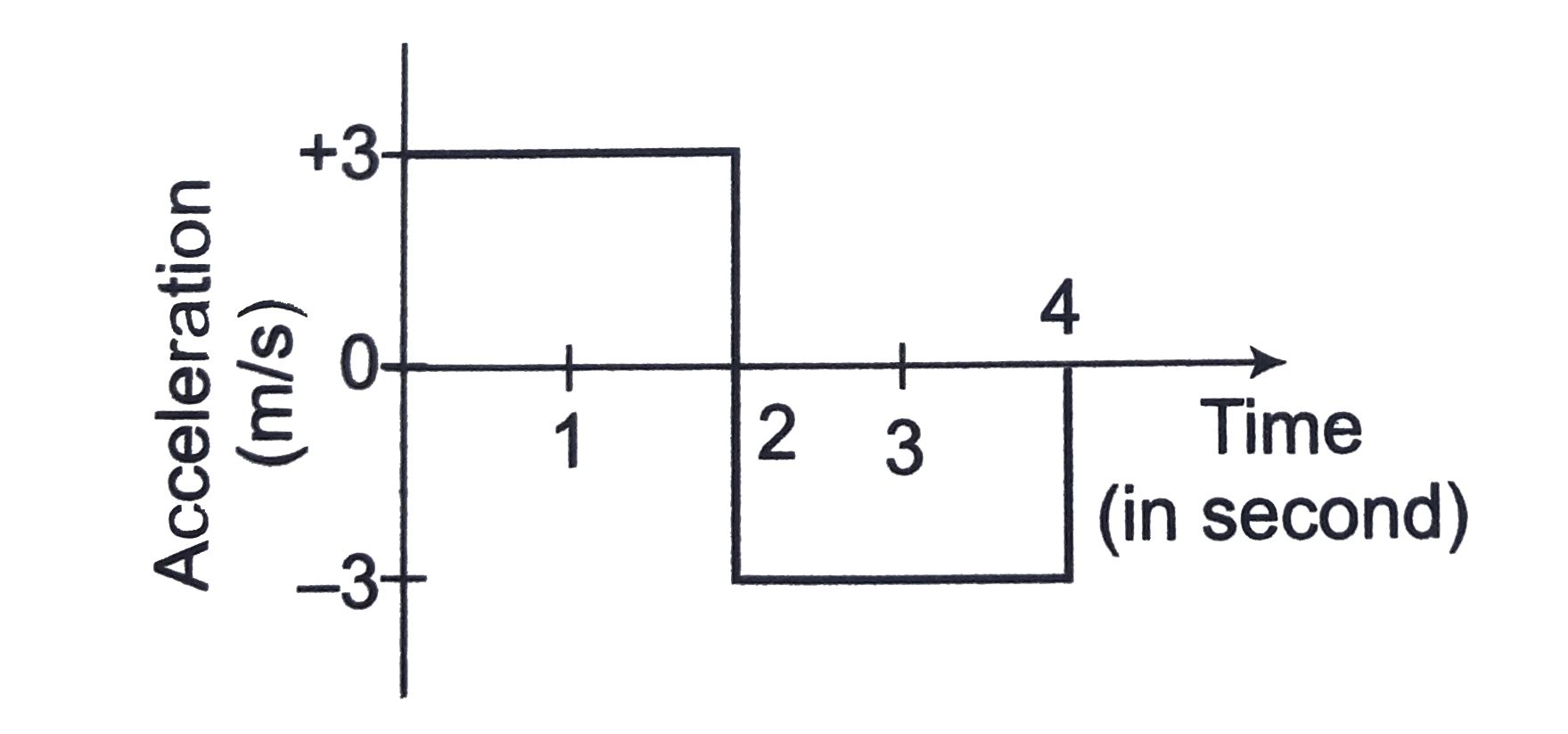 View Solution
View SolutionA particle, starting from rest, moves in a straight line with constant acceleration a0 for a time interval t0.Then is accelerates at a constant rate 2a0 for time interval 2t0 .The distance travelled by the particle in time 3t0 from the starts is S . Then Sa0t20=
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
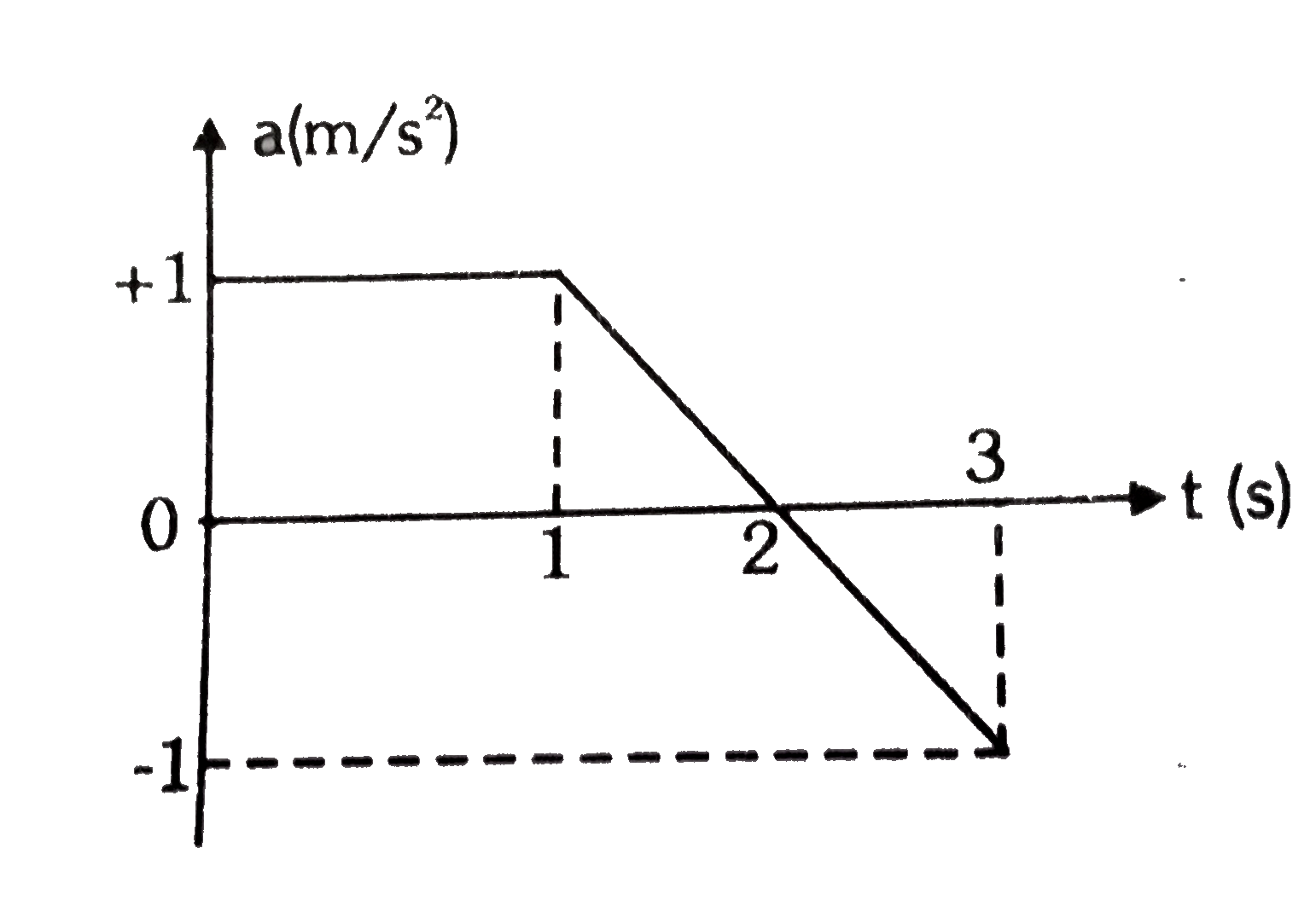 View Solution
View SolutionA particle starts from rest with constant acceleration. The ratio of space-average velocity to the time average velocity is :-
View SolutionA particle starts moving from position of rest under a constant acceleration. If it travels a distance x in t second, what distance will it travel in next t second?
View SolutionA particle starts motion from rest and moves along a straight line. Its velocity-time graph is shown. Find out speed of particle at t=2s and at t=3s.
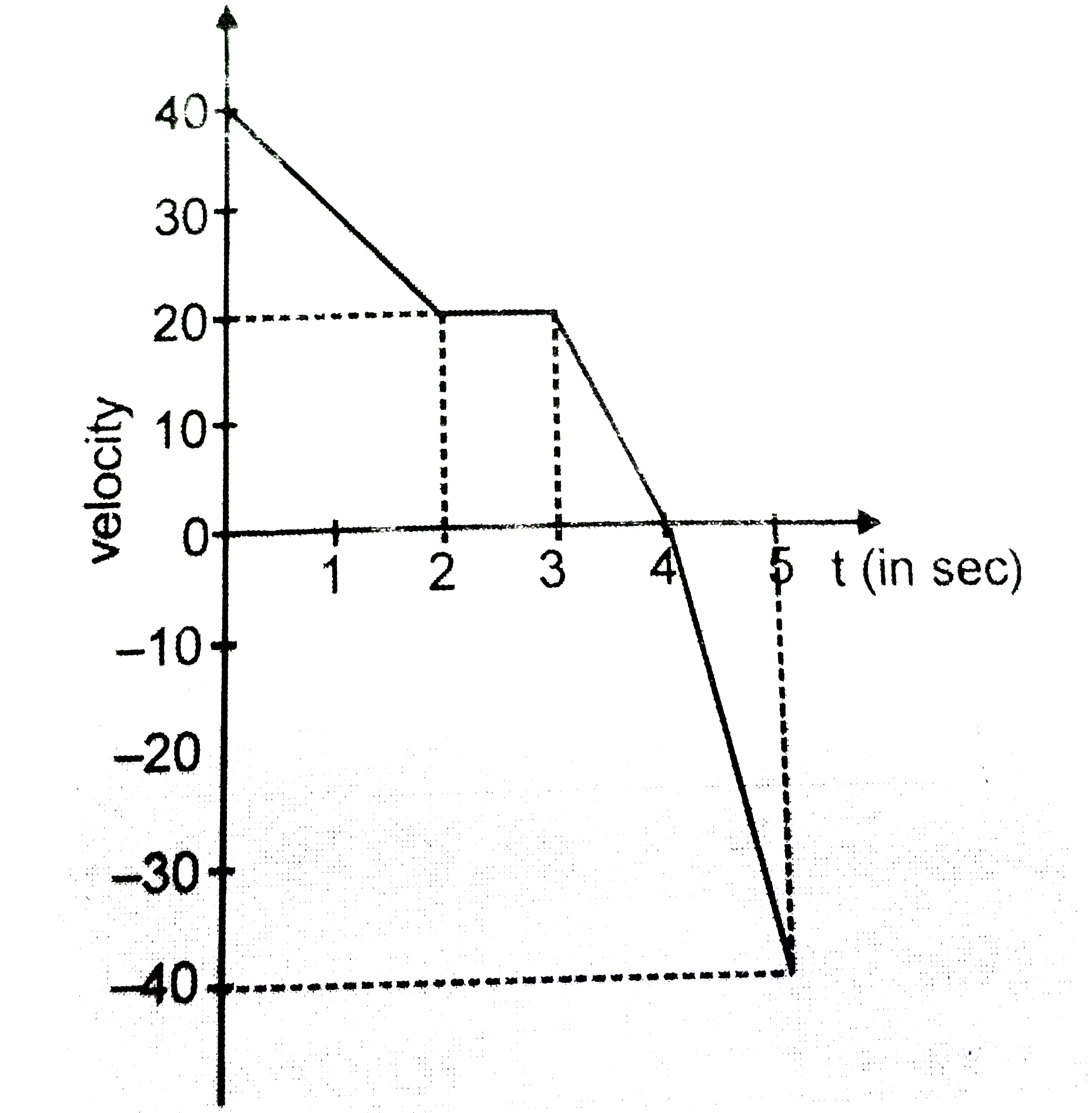 View Solution
View SolutionA particle starting from rest moves with constant acceleration. If it takes 5.0 s to reash the speed 18.0 km/h find a. the average velocity during this period, and b. the distance travelled by the particle during this period.
View Solution
