A particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is
12kt2
12at2
16at2
None
The correct Answer is:C
To solve the problem, we need to find the displacement s of a particle that starts from rest and moves with an acceleration that varies with time as a=kt, where k is a constant.
1. Understand the relationship between acceleration, velocity, and displacement:
- We know that acceleration a is the derivative of velocity v with respect to time t:
a=dvdt
2. Substitute the given acceleration:
- Given a=kt, we can write:
dvdt=kt
3. Integrate to find velocity:
- To find the velocity v, we integrate both sides with respect to t:
dv=ktdt
- Integrating gives:
v=∫ktdt=kt22+C
- Since the particle starts from rest, the initial velocity v(0)=0, so C=0. Thus, we have:
v=kt22
4. Relate velocity to displacement:
- We know that velocity v is also the derivative of displacement s with respect to time:
v=dsdt
- Substituting for v:
dsdt=kt22
5. Integrate to find displacement:
- Now we integrate to find the displacement s:
ds=kt22dt
- Integrating gives:
s=∫kt22dt=k2⋅t33+C
- Again, since the particle starts from rest, the initial displacement s(0)=0, so C=0. Thus, we have:
s=kt36
Final Answer:
The displacement s of the particle at time t is:
s=kt36
- We know that acceleration a is the derivative of velocity v with respect to time t:
a=dvdt
- Given a=kt, we can write:
dvdt=kt
- To find the velocity v, we integrate both sides with respect to t:
dv=ktdt
- Integrating gives:
v=∫ktdt=kt22+C
- Since the particle starts from rest, the initial velocity v(0)=0, so C=0. Thus, we have:
v=kt22
- We know that velocity v is also the derivative of displacement s with respect to time:
v=dsdt
- Substituting for v:
dsdt=kt22
- Now we integrate to find the displacement s:
ds=kt22dt
- Integrating gives:
s=∫kt22dt=k2⋅t33+C
- Again, since the particle starts from rest, the initial displacement s(0)=0, so C=0. Thus, we have:
s=kt36
The displacement s of the particle at time t is:
s=kt36
Topper's Solved these Questions
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Advance MCQs with One or More Options Correct
17 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Conceptual MCQs Single Option Correct
35 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
Similar Questions
A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of time in successive displacement d.
View SolutionThe acceleration of a particle, starting from rest, varies with time according to relation , a=−rω2sinomηt. Find the displacemnt of this particle at a time (t).
View Solution
Knowledge Check
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A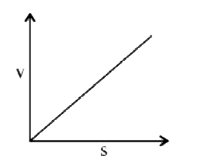 B
B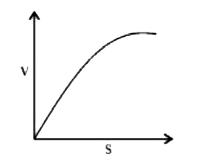 C
C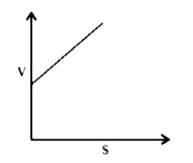 D
D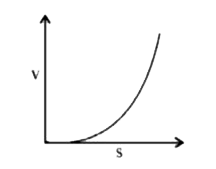
A particle of mass m impves along a horzontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Total force on particle at time t s isAm√k(R2+kt4)Bm√k(R+kt4)C2m√k(R+kt4)Dm2√k(R+kt4)A particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
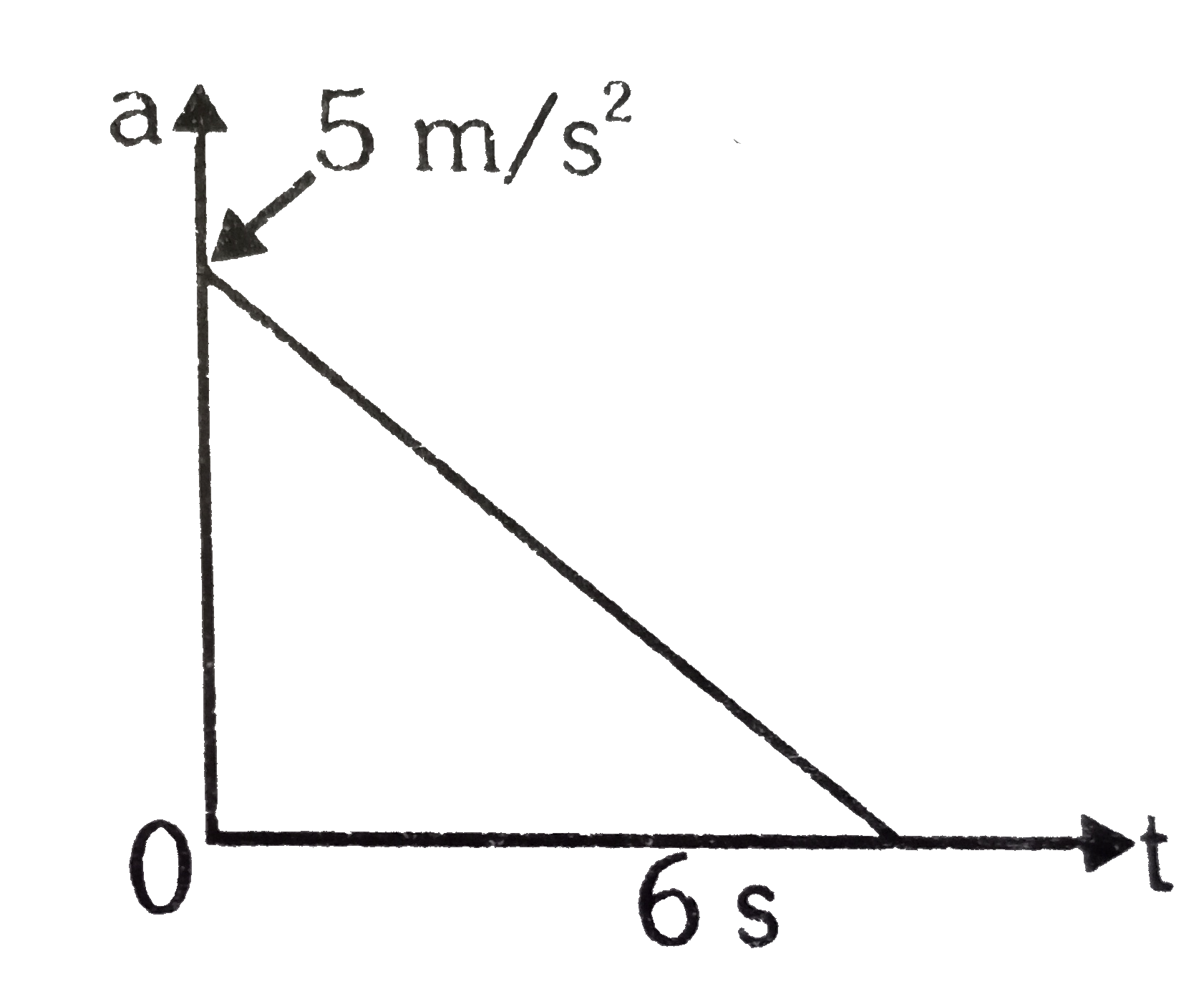 A7.5m/sB15m/sC30m/sD37.5 m/s
A7.5m/sB15m/sC30m/sD37.5 m/s
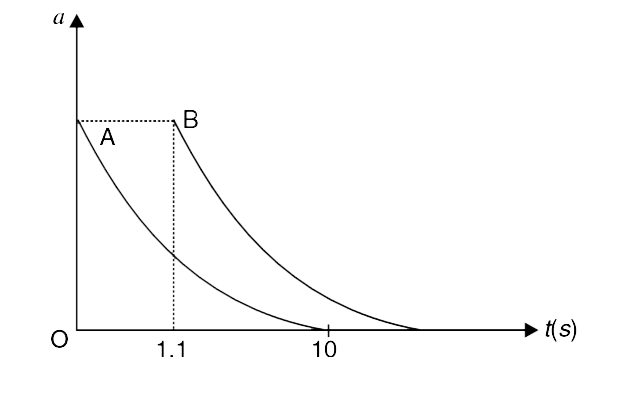
Particle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle of mass m impves along a horzontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Tangential force on particle at t s is
View SolutionA particle of mass m impves along a horzontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Power developed by total at time t is
View SolutionA particle starts from rest and has velocity kt after time t. The distance travelled in time t is-
View Solution
