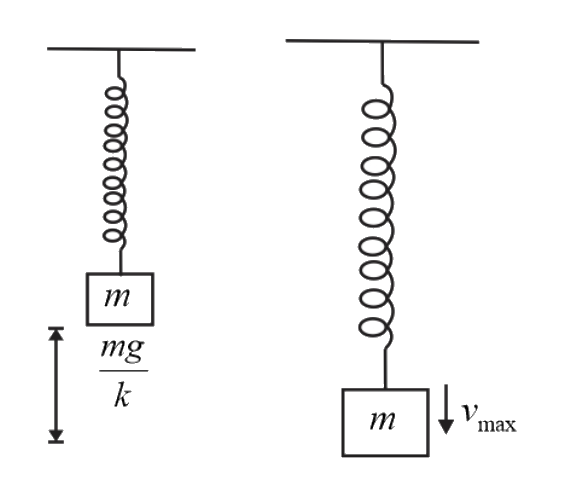
A particle suspended from a vetical spring oscillastes 10 times per sencon. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretche by 0.20 cm. Take $g = π^{2} m s^{- 2}$

Video Solution

Text Solution

Verified by Experts

a. The mea position of the particle durig vertical oscillsations is $m \frac{g}{k}$ distance away from its position when the sprig is unstretched. At the highest point i.e. at an extreme positon, the spring is unstretched.

hence the amplitude is
$A = \frac{m g}{k}$ ..............i
The angular frequency is
$ω = \sqrt{\frac{k}{m}} = 2 π v = (20 π) s^{- 1}$ ........ii
or $\frac{m}{k} = \frac{1}{40 π^{2}} s^{2}$
Putting in i the amplitude is
$A = (\frac{1}{400 π^{2}} s^{2}) (π^{2} \frac{m}{s^{2}})$
$= \frac{1}{400} m = 0.25 c m$
The maximum speed $= A ω$
k $= (0.25 c m) (20 π s^{- 1}) = 5 π c m s^{- 1}$
b. When the spring is stretched by 0.20 cm the block is 0.25 cm-0.20 cm=0.05 cm above the meann position. The speed at this positioin will be
$v = ω \sqrt{A^{2} - x^{2}}$
$= (20 π s^{- 1}) (\sqrt{{(0.25 c m)}^{2} - {(0.05 c m)}^{2}}$
$= 15.4 c m s^{- 1}$

Updated on:21/07/2023