A particle with the position vector r has linear momentum p. Which of the following statements is true is respect of its angular momentum L about the origin ?
L acts along p
L acts along r
L is maximum when p and r are parallel
L is maximum when p is perpendicular to r
The correct Answer is:D
To solve the problem regarding the angular momentum L of a particle with position vector r and linear momentum p, we can follow these steps:
1. Understanding Angular Momentum:
The angular momentum L of a particle about the origin is given by the cross product of the position vector r and the linear momentum p:
L=r×p
2. Properties of the Cross Product:
The magnitude of the angular momentum can be expressed as:
|L|=|r||p|sinθ
where θ is the angle between the vectors r and p.
3. Direction of Angular Momentum:
The direction of the angular momentum vector L is given by the right-hand rule, which indicates that L is perpendicular to both r and p. Therefore, options stating that L acts along p or r are incorrect.
4. Maximizing Angular Momentum:
The magnitude of L is maximized when sinθ is maximized. The maximum value of sinθ is 1, which occurs when θ=90∘ (or π2 radians). This means that the vectors r and p must be perpendicular to each other for L to be maximized.
5. Evaluating the Options:
- Option 1: L acts along p → Incorrect (as L is perpendicular to p).
- Option 2: L acts along r → Incorrect (as L is perpendicular to r).
- Option 3: L is maximum when p and r are parallel → Incorrect (as this would make θ=0 and L=0).
- Option 4: L is maximum when p is perpendicular to r → Correct (as this gives θ=90∘).
6. Conclusion:
The correct answer is that the angular momentum L is maximum when the linear momentum p is perpendicular to the position vector r.
Final Answer:
The correct statement is Option 4: L is maximum when p is perpendicular to r.
The angular momentum L of a particle about the origin is given by the cross product of the position vector r and the linear momentum p:
L=r×p
The magnitude of the angular momentum can be expressed as:
|L|=|r||p|sinθ
where θ is the angle between the vectors r and p.
The direction of the angular momentum vector L is given by the right-hand rule, which indicates that L is perpendicular to both r and p. Therefore, options stating that L acts along p or r are incorrect.
The magnitude of L is maximized when sinθ is maximized. The maximum value of sinθ is 1, which occurs when θ=90∘ (or π2 radians). This means that the vectors r and p must be perpendicular to each other for L to be maximized.
- Option 1: L acts along p → Incorrect (as L is perpendicular to p).
- Option 2: L acts along r → Incorrect (as L is perpendicular to r).
- Option 3: L is maximum when p and r are parallel → Incorrect (as this would make θ=0 and L=0).
- Option 4: L is maximum when p is perpendicular to r → Correct (as this gives θ=90∘).
The correct answer is that the angular momentum L is maximum when the linear momentum p is perpendicular to the position vector r.
The correct statement is Option 4: L is maximum when p is perpendicular to r.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Angular momentum(L) is one of the following?
View SolutionA particle of mass m is moving along the side of a square of side a, with a uniform speed v in XY plane as shown in Fig. Which of the followig statements is false for the angular momentum →L about the origin?
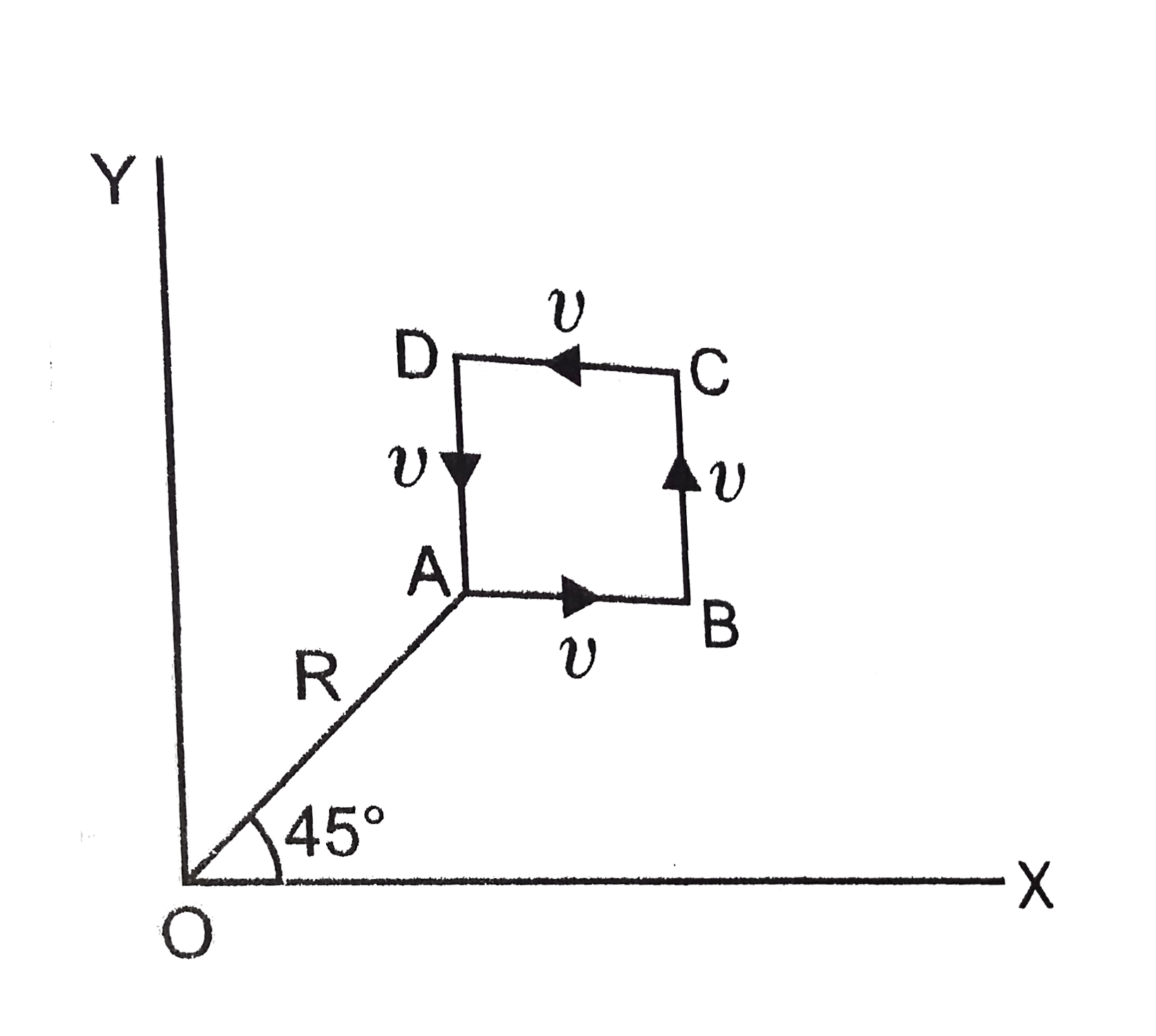
View SolutionIf for some particle its position vector and linear momentum are respectively be 2ˆi+ˆj+ˆk and 2ˆi−3ˆj+ˆk. Its angular momentum will be:
View SolutionA particle moving in a circular path has an angular momentum of L. If the frequency of rotation is halved, then its angular momentum becomes
View SolutionA particle of mass m is travelling with a constant velocity v=v0ˆi along the line y=b,z=0. Let dA be the area swept out by the position vector from origin to the particle in time dt and L the magnitude of angular momentum of particle about origin at any time t. Then
View SolutionAssertion : If a particle moves with a constant velocity, then angular momentum of this particle about any point remains constant.
Reason : Angular momentum has the units of Plank's constant.
View SolutionIf a moving particle have linear momentum ¯¯¯P and position vector ¯r then choose the correct relation between ¯r,¯p and angular momentum ¯¯¯L of particle about the origin.
View SolutionA particle moves in space such that its position vector varies as →r=2tˆi+3t2ˆj. If mass of particle is 2 kg then angular momentum of particle about origin at t=2 sec is
View SolutionA particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View SolutionA rigid body rotates with an angular momentum L. If its rotational kinetic energy is made 4 times, its angular momentum will become
View Solution
