A passengee is traveling a train moving at 40ms−1 Hit suitcase is kept on the berth ,The drive of train applies breaks such that the speed of the train decreases at a constant rate to 20ms−1 in 5s What should be the minimum coefficient of friction between the suitcase and the berth if the suitcase is not to slide during and retardation of the train ?
0.3
0.5
0.1
0.2
The correct Answer is:b
To solve the problem step by step, we need to determine the minimum coefficient of friction required to prevent the suitcase from sliding on the berth during the train's deceleration.
Step 1: Calculate the Retardation of the Train
The train's speed decreases from 40m/s to 20m/s in 5s. We can calculate the retardation (deceleration) using the formula:
a=vf−vit
Where:
- vf=20m/s (final velocity)
- vi=40m/s (initial velocity)
- t=5s (time)
Substituting the values:
a=20m/s−40m/s5s=−20m/s5s=−4m/s2
The negative sign indicates that this is a deceleration.
Step 2: Understand the Forces Acting on the Suitcase
For the suitcase to not slide, the frictional force must be sufficient to provide the necessary acceleration (retardation in this case) to the suitcase. The frictional force Ff can be expressed as:
Ff=μmg
Where:
- μ is the coefficient of friction
- m is the mass of the suitcase
- g is the acceleration due to gravity (g≈10m/s2)
Step 3: Set Up the Equation for Forces
The suitcase must experience a backward acceleration of 4m/s2 (the same as the train's retardation). The net force required to achieve this acceleration is given by:
F=ma=m⋅4
Step 4: Equate the Frictional Force to the Required Force
For the suitcase not to slide, the frictional force must be equal to or greater than the force required to accelerate the suitcase:
μmg≥ma
Cancelling m from both sides (assuming m≠0) gives:
μg≥a
Step 5: Solve for the Coefficient of Friction
Substituting g=10m/s2 and a=4m/s2:
μ⋅10≥4
Dividing both sides by 10:
μ≥410=0.4
Conclusion
The minimum coefficient of friction required to prevent the suitcase from sliding is:
μ≥0.4
The train's speed decreases from 40m/s to 20m/s in 5s. We can calculate the retardation (deceleration) using the formula:
- vf=20m/s (final velocity)
- vi=40m/s (initial velocity)
- t=5s (time)
For the suitcase to not slide, the frictional force must be sufficient to provide the necessary acceleration (retardation in this case) to the suitcase. The frictional force Ff can be expressed as:
- μ is the coefficient of friction
- m is the mass of the suitcase
- g is the acceleration due to gravity (g≈10m/s2)
The suitcase must experience a backward acceleration of 4m/s2 (the same as the train's retardation). The net force required to achieve this acceleration is given by:
For the suitcase not to slide, the frictional force must be equal to or greater than the force required to accelerate the suitcase:
Substituting g=10m/s2 and a=4m/s2:
The minimum coefficient of friction required to prevent the suitcase from sliding is:
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A motercyclist wants to drive on the vertical surface of wooden 'well' of radius 5 m, with a minimum speed of 5√5ms−1. The minimum value of coefficient of friction between the tyres and the well must be (take, g = 10ms−2)
View SolutionA train moving with a velocity of 20 m s−1' is brought to rest by applying brakes in 5 s. Calculate the retardation.
View SolutionThe driver of a train moving at 72kmh−1 sights another train moving at 4ms−1 on the same track and in the same direction. He instantly applies brakes to produces a retardation of 1ms−2. The minimum distance between the trains so that no collision occurs is
View SolutionAn empty luggage carrier A of mass M=40kg slide without friction on horizontal floor hits with a velocity v0=5ms−1 an identical carrier B containing m=15 kg suitacase. The impact causes the suitcase to slide on the floor of carrier B and collide with the left wall of carrier B. knowing that the coefficient of restitution between the two carriers is 0.80 and that the coefficient of restitution between the suitcase and the wall of carriere B is 2/9. Assume no friction any where. Find
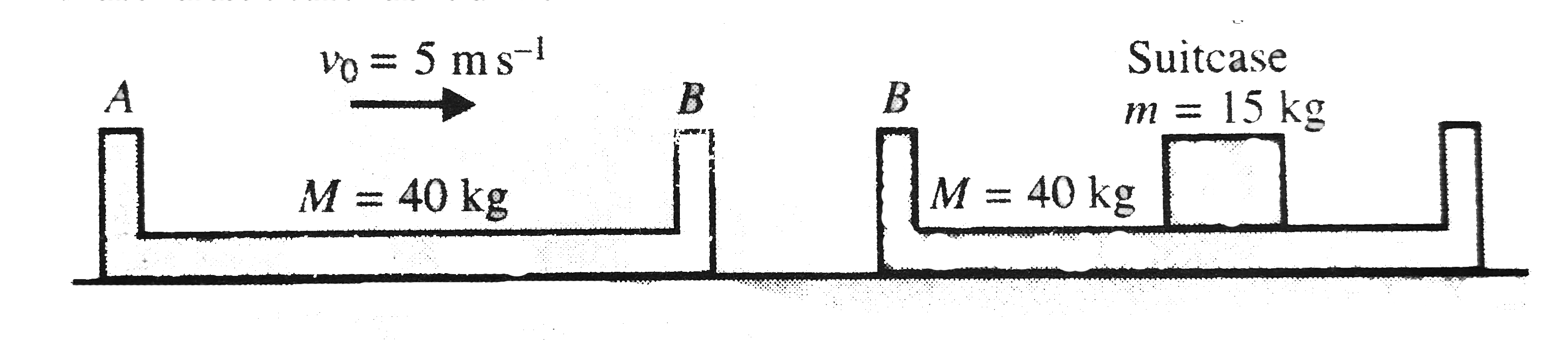
a. the velocities of carrier A and carrier B just after collision.
b. the velocity of carrier B after the suitcase its the wall for the first time is
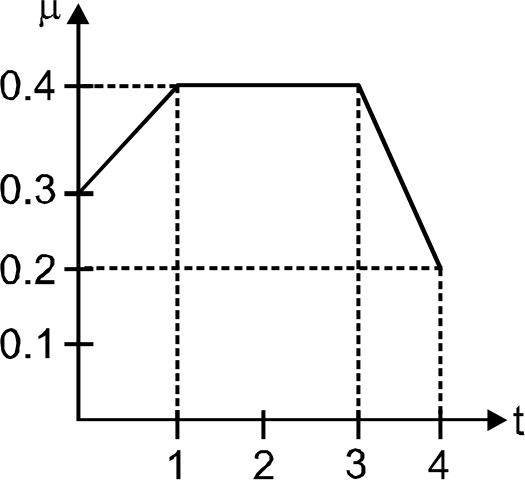
View SolutionA small body is projected with a velocity of 20.5ms−1 along rough horizontal surface. The coefficient of friction (μ) between the body and surface changes with time t (in s) as the the body moves along the surface. Find the velocity at the end of 4s in m/s
View SolutionA track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2

View SolutionA train is moving at a speed of 5515 km/h. The train travels at the same speed for 6 hours 40 minutes. What is the distance covered by the train?
View SolutionA train is moving at a constant speed V when its driverobserves another train in front of him on the same track and voing in the same direction with constant speed v. If the distance berween the trains is x. Trains is x then what should be the minimum retardation of the train so as to avoed collision?.
View SolutionTwo trains are moving with velocities v1=10ms−1andv2=20ms−1 on the same track in opposite directions. After the application of brakes if their retarding rates are a1=2ms−2anda2=1ms−2 respectively, then the minimum distance of separation between the trains to avoid collision is
View SolutionA thin rod of length 1m is fixed in a vertical position inside a train, which is moving horizentally with constant acceleration 4ms−2.A bead can slide on the rod and friction coefficient between them is 0.5. If the head is released from rest at the top of the rod , it will reach the bottom the in
View Solution
