A pendulum is constructed as a light thin− walled sphere of radius R filled up with water and suspended at the point O from a light rigid rod (figure). The distance between the point O and the centre of the sphere is equal to l. How many times will the small oscillations of such a pendulum change after the water freezes ? The visxosity of water and the change of its volume on freezes? The viscosity of water and the change of its volume on freezing are to be necglected.
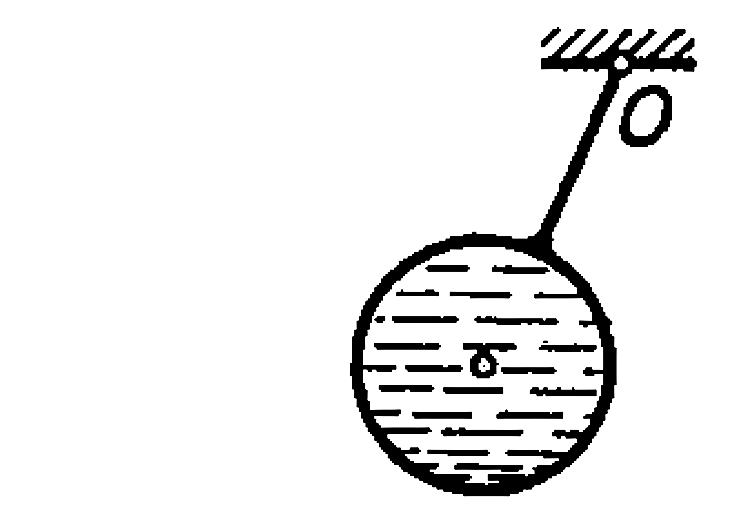
If water has frozen, the system consisting of the light rod and the frozen water in the hollow sphere constitute a compound (physical ) pendulum to a very good approximation because we can take the whole system to be rigid. For such systems the time period is given by
T1=2π√lg√1+k2l2 wherek2=25R2 is the radius of gyration of the sphere. The situation is different when water is unfrozen. When dissipative froces (viscosity) are neglected, we are dealing with idal fluids. Such fluids instantaneously respond to ( unbalanced ) internal stresses. Suppose the sphere with liquid water actually executes small rigid oscillation. Then the portion of the fluid above the centre of the sphere will have a greater acceleration than the portion below the centre because the linear acceleratino of any element is in this case, equal to angular acceleration of the element multiplied by the distance of the element from the centre of suspension ( Recall that we are considering small oscillations ). Then, as is obvious in a frame moving with the centre of mass, there will appear an unbalanced couple ( not negated by any pseudoforces ) which will cause the fluid to move rotationally so as to destroy in acceleration. Thus for this case of ideal fluids the pendulum must in such a way that the elements of the fluid all undergo the same acceleration. This implies that we have a simple ( mathematical ) pendulum with the time period :
T0=2π√lm
Thus T1=T0√1+25(Rl)2
( One expects that a liquid with very small viscosity will have a time period close T0 while one with high viscosity will have a time period closer to T1).
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
How will the frequency of small oscillation of a simple pendulum changes.
If it moves vertically upward with an acceleration 'a'
View SolutionHow will the frequency of small oscillation of a simple pendulum changes.
If it moves vertically down with acceleration a<g or with acceleration a>g
View Solution
Knowledge Check
The radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
ARB0.5RC√0.6RD√0.3RThe distance between the points of suspension and centre of oscillation for a compound pendulum is :
Ak2−l22Bk2+l2lCk2+l22lDk+l2kA thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
A12mB34mC1 mD23m
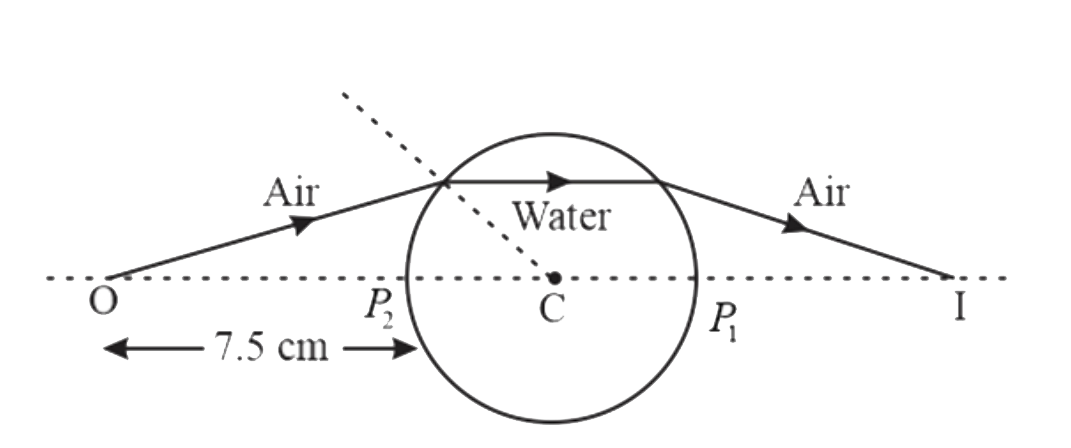
A thin walled glass sphere of radius 2.5 cm is filled with water. An object (O) is placed at 7.5 cm from the effect of glass wall, at what distance the image (I) of the object , measured from the centre of sphere is formed ? (refractive index of water = 1.333)
View SolutionHow will the frequency of small oscillation of a simple pendulum changes.
a point of suspension moves horizontally in the plane of oscillation with acceleration a.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionHow will the frequency of small oscillation of a simple pendulum changes.
in which case, if at all, is analogous to a pendulum mounted on a cart rolling down an inclined plane.
View SolutionA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
View Solution
