A person with body resistance between his hands of 10KΩ accidentally grasps the terminals of a 18kV power supply.
(i) If the internal resistance of the power supply is 2000Ω, what is the power dissipated in his body?
(ii) What is the power dissipated in his body?
(iii) If the power supply is to be made safe by increasing its internal resistance, what should the internal resistance be for the maximum current in the above situation to be 1.00mA or less?
To solve the problem step by step, we will break it down into three parts as per the question.
Given Data:
- Body resistance Rb=10kΩ=10×103Ω
- Power supply voltage V=18kV=18×103V
- Internal resistance of the power supply Ri=2000Ω
Part (i): Calculate the Power Dissipated in the Body
1. Calculate Total Resistance in the Circuit:
Rtotal=Rb+Ri=10×103+2000=10,000+2000=12,000Ω
2. Calculate the Current (I) through the Circuit:
Using Ohm's Law:
I=VRtotal=18×10312×103=1812=1.5A
3. Calculate Power Dissipated in the Body:
The power dissipated in the body can be calculated using the formula:
P=I2Rb
Substituting the values:
P=(1.5)2×(10×103)=2.25×10,000=22,500W=22.5kW
Part (ii): Power Dissipated in the Body
The power dissipated in the body is already calculated in Part (i):
P=22.5kW
Part (iii): Determine the Required Internal Resistance for Maximum Current of 1 mA
1. Set the Desired Current (I):
I=1mA=1×10−3A
2. Use Ohm's Law to Find the Required Total Resistance:
V=I×Rtotal
Rearranging gives:
Rtotal=VI=18×1031×10−3=18×106Ω
3. Calculate the Required Internal Resistance (R_i):
The total resistance Rtotal is the sum of body resistance and internal resistance:
Rtotal=Rb+Ri
Rearranging gives:
Ri=Rtotal−Rb=18×106−10×103=18×106−10,000
Since 10,000 is negligible compared to 18×106:
Ri≈18×106Ω=18MΩ
Final Answers:
(i) Power dissipated in the body: 22.5kW
(ii) Power dissipated in the body: 22.5kW
(iii) Required internal resistance for maximum current of 1mA: 18MΩ
- Body resistance Rb=10kΩ=10×103Ω
- Power supply voltage V=18kV=18×103V
- Internal resistance of the power supply Ri=2000Ω
Rtotal=Rb+Ri=10×103+2000=10,000+2000=12,000Ω
Using Ohm's Law:
I=VRtotal=18×10312×103=1812=1.5A
The power dissipated in the body can be calculated using the formula:
P=I2Rb
Substituting the values:
P=(1.5)2×(10×103)=2.25×10,000=22,500W=22.5kW
The power dissipated in the body is already calculated in Part (i):
P=22.5kW
I=1mA=1×10−3A
V=I×Rtotal
Rearranging gives:
Rtotal=VI=18×1031×10−3=18×106Ω
The total resistance Rtotal is the sum of body resistance and internal resistance:
Rtotal=Rb+Ri
Rearranging gives:
Ri=Rtotal−Rb=18×106−10×103=18×106−10,000
Since 10,000 is negligible compared to 18×106:
Ri≈18×106Ω=18MΩ
(i) Power dissipated in the body: 22.5kW
(ii) Power dissipated in the body: 22.5kW
(iii) Required internal resistance for maximum current of 1mA: 18MΩ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.122videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective8videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type4videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
Similar Questions
If the power dissipated in 5Ω is 20 W then power dissipated in 4Ω is -
 View Solution
View SolutionIf the power dissipated in the circuit is 4W then the value of R is:
_2019_CBT7_E01_014_Q01.png) View Solution
View SolutionIf the power dissipated in the circuit is 4W then the value of R is:
_2019_CBT7_E01_014_Q01.png) View Solution
View SolutionFor maximum power from battery the internal resistance of battery r is
 View Solution
View SolutionIf in the circuit, power dissipation is 150 W, then R is :
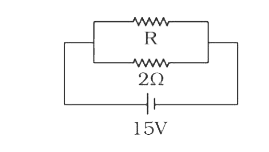 View Solution
View SolutionIf in the circuit, power dissipation is 150W, the R is
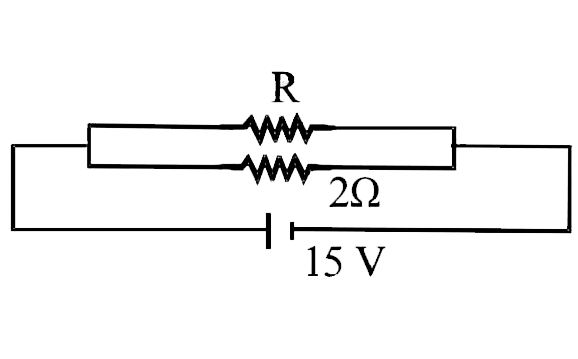 View Solution
View SolutionResistors P,Q,andR in the circuit have equal resistances. If the battery is supplying a total power of 12W , what is the power dissipated as heat in resistors R?
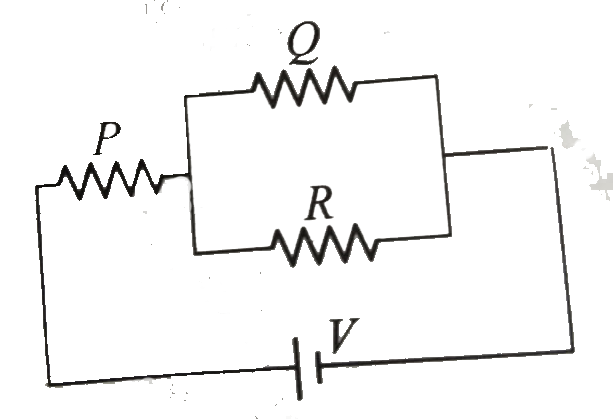 View Solution
View SolutionThe power dissipated (in watt) in 3Ω resistance in the following circuit is
 View Solution
View SolutionThe maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
View SolutionIn the network shown in the figure, power dissipated in 3Ω and 12 W. Power dissipated in 4Ω will be
 View Solution
View Solution

