A planet of radius R=110×(radiusofEarth) has the same mass density as Earth. Scientists dig a well of depthR5 on it and lower a wire of the same length and a linear mass density 10−3kgm(_1) into it. If the wire is not touching anywhere, the force applied at the top of the wire by a person holding it inplace is (take the radius of Earth=6×106m and the acceleration due to gravity on Earth is 10ms−2
96N
108N
120N
150N
The correct Answer is:B
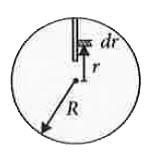
Gravitational field inside the planet at a distance r from centre,
gi=GMR3r=G(43πR3)ρR3r=43Gπrρ
Force applied by the person on the wire at rest is the weight of the wire. Since, gravitational field is variable so force on each part of the wire is different. Consider a small portion dr of the wire at a distance r from centre of the planet, so its weight will be
dW=(dm)gi=(λdr)(43Gπrρ)=(43Gπρ)(λrdr)
Net weight , W=∫dW=(43Gπρλ)∫R4R5rdr
W=(43Gπρλ)(950)R2
Density of the earth , ρME43πR3E, also , R=RE10
Putting the values of ρ and R in equation (i) , we get
W=(95×103)gEλRE=95×103×10×10−3×6×106=108N
so , net force applied by the person to hold the wire = 108N
Topper's Solved these Questions
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)
19 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)
6 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)
9 Videos
- BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYBOOK - MTG GUIDECHAPTER - BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYEXERCISE - AIPMT / NEET (MCQs)
11 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
Similar Questions
A wire having a linear mass density 5.0×1003kgm−1 is stretched between two rigid supportes with a tension of 450 N. The wire resonates at which the same wire resontes is 490 Hz. Find the length of the wire.
View SolutionTwo wires of same material and radius have their lengths in ratio 1 : 2. If these wires are stretched by the same force, the strain produced in the two wires will be in the ratio
View Solution
Knowledge Check
If the density of the planet is double that of the earth and the radius 1.5 times that of the earth, the acceleration due to gravity on the planet is
A4/3 times that on the surface of the earthB3 times that on the surface of the earthC3/4 times that on the surface of the earthD6 times that on the surface of the earthWhen 115V is applied across a wire that is 10m long and has a 0.30mm radius, the current density is 1.4×104A/m2. The resistivity of the wire is
A2.0×10−4ΩmB4.1×10−4ΩmC8.2×10−4ΩmD2.0×10−3ΩmTwo wires of same material and radius have their lengths in ratio 1 : 2. If these wires are stretched by the same force, the strain produced in the two wires will be in the ratio
A2 : 1B1 : 1C1 : 2D1 : 4
A force F is applied on the wire of radius r and length L and change in the length of wire is l. If the same force F is applied on the wire of the same material and radius 2r and length 2L. Then the change in length of the other wire is
View SolutionThe mass and length of a wire are M and L respectively. The density of the material of the wire is d. On applying the force F on the wire, the increase in length is l, then the Young's modulus of the material of the wire will be
View SolutionIn a hypothetical situation, the density of earth becomes three times that of its original density, but its radius remains same. The acceleration due to gravity becomes : (take g=10m/s2 on the earth)
View SolutionA wire having a linear mass density 5×10−3 kg/m is stretched between two rigid supports with a tension of 450 N. The wire resibate at a frequency of 420 Hz. The next higher frequency at which the same wire resonates is 490 Hz. Find the length of wire -
View SolutionA force F is needed to break a copper wire having radius R. The force needed to break a copper wire of same length and radius 2R will be
View Solution
