A plank fitted with a gun is moving on a horizontal surface with speed of 4m/s along the positive x-axis. The z-axis is in vertically upward direction. The mass of the plank including the mass of the gun is 50 kg. When the plank reaches the origin, a shell of mass 10 kg is fired at an angle of 60∘ with the positive x-axis with a speed of v=20m/s with respect to the gun in x-z plane. Find the position vector of the shell at t=2 s after firing it. Take g=9.8m/s2.
The correct Answer is:A, B, D
To solve the problem, we need to find the position vector of the shell at t=2 seconds after it is fired. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Initial Conditions
- The plank (including the gun) is moving with a speed of 4m/s along the positive x-axis.
- The shell is fired at an angle of 60∘ with respect to the positive x-axis with a speed of 20m/s relative to the gun.
Step 2: Determine the Velocity of the Shell
The velocity of the shell can be determined by combining the velocity of the plank and the velocity of the shell relative to the plank.
1. Velocity of the shell in the x-direction:
vx=vplank+vshell⋅cos(60∘)
vx=4m/s+20⋅cos(60∘)=4+20⋅12=4+10=14m/s
2. Velocity of the shell in the z-direction:
vz=vshell⋅sin(60∘)
vz=20⋅sin(60∘)=20⋅√32=10√3m/s
Step 3: Calculate the Position of the Shell at t=2 seconds
Now, we can calculate the position of the shell in both x and z directions at t=2 seconds.
1. Position in the x-direction:
x(t)=vx⋅t=14⋅2=28m
2. Position in the z-direction:
Using the second equation of motion for vertical motion:
z(t)=vz⋅t−12gt2
z(t)=(10√3)⋅2−12⋅9.8⋅(22)
z(t)=20√3−12⋅9.8⋅4
z(t)=20√3−19.6
Approximating √3≈1.732:
z(t)≈20⋅1.732−19.6≈34.64−19.6≈15.04m
Step 4: Write the Position Vector
The position vector →r of the shell at t=2 seconds is given by:
→r=x(t)^i+z(t)^k=28^i+15.04^km
Final Answer
The position vector of the shell at t=2 seconds after firing it is:
→r=28^i+15.04^km
- The plank (including the gun) is moving with a speed of 4m/s along the positive x-axis.
- The shell is fired at an angle of 60∘ with respect to the positive x-axis with a speed of 20m/s relative to the gun.
The velocity of the shell can be determined by combining the velocity of the plank and the velocity of the shell relative to the plank.
vx=vplank+vshell⋅cos(60∘)
vx=4m/s+20⋅cos(60∘)=4+20⋅12=4+10=14m/s
vz=vshell⋅sin(60∘)
vz=20⋅sin(60∘)=20⋅√32=10√3m/s
Now, we can calculate the position of the shell in both x and z directions at t=2 seconds.
x(t)=vx⋅t=14⋅2=28m
Using the second equation of motion for vertical motion:
z(t)=vz⋅t−12gt2
z(t)=(10√3)⋅2−12⋅9.8⋅(22)
z(t)=20√3−12⋅9.8⋅4
z(t)=20√3−19.6
Approximating √3≈1.732:
z(t)≈20⋅1.732−19.6≈34.64−19.6≈15.04m
The position vector →r of the shell at t=2 seconds is given by:
→r=x(t)^i+z(t)^k=28^i+15.04^km
The position vector of the shell at t=2 seconds after firing it is:
→r=28^i+15.04^km
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
Knowledge Check
A shell of mass 200g is fired by a gun of mass 100kg. If the muzzle speed of the shell is 80ms−1 , then the rcoil speed of the gun is
A16cms−1B8cms−1C8ms−1D16ms−1
A particle of mass m is projected from origin O with speed u at an angle θ with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time t about O before the particle strikes the ground again.
View SolutionA shell of mass 0.01 kg fired by a gun of mass 10 kg. If the muzzle speed of the shell is 50ms−1, what is the recoil speed of the gun?
View SolutionA shell of mass 0.020 kg is fired by a gun of mass 100 kg. If the speed of the shell is 80ms, the recoil speed of the gun would be
View SolutionA shell of mass 0.02 kg is fird by a gun of mass 10 kg. If the muzzle speed of the shell is 600 ms−1, what is the recoil speed of the gun?
View SolutionA plank of mass m moving with a velocity v along a friction less horizontal track and a body of mass m/2 moving with 2v collides with plank elastically. Final speed of the plank is:
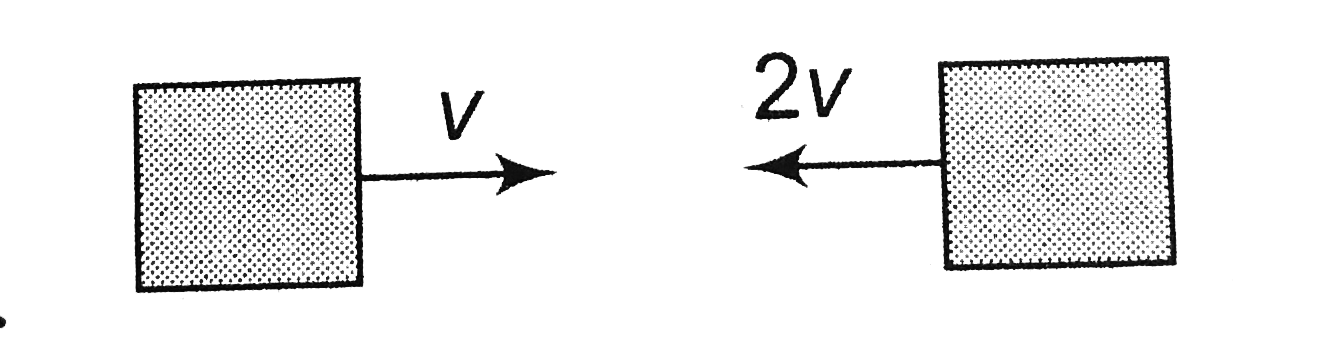
View SolutionA machine gun has a mass of 20kg. It fires 35 g bullets at the rate of 4 bullets per second, with a speed of 400ms−1. What force must be applied to the gun to keep it in position?
View SolutionA bullet of mass 10 g is fired from a gun of mass 1 kg with recoil velocity of gun 5 m/s. The muzzle velocity will be
View Solution
