A plank of mass $M$ is placed on a rough horizontal surface and a contant horizontal force $F$ is applied on it . A man of mass $m$ runs on the plank find the range of acceleration of the man that the plank does not move on the surface is $μ$ .Assume that the does not slip on the plank

Video Solution

Text Solution

Verified by Experts

Here $f_{1} =$ force of friction between man and plank $f_{2} =$ force of friction between man and plank and surface

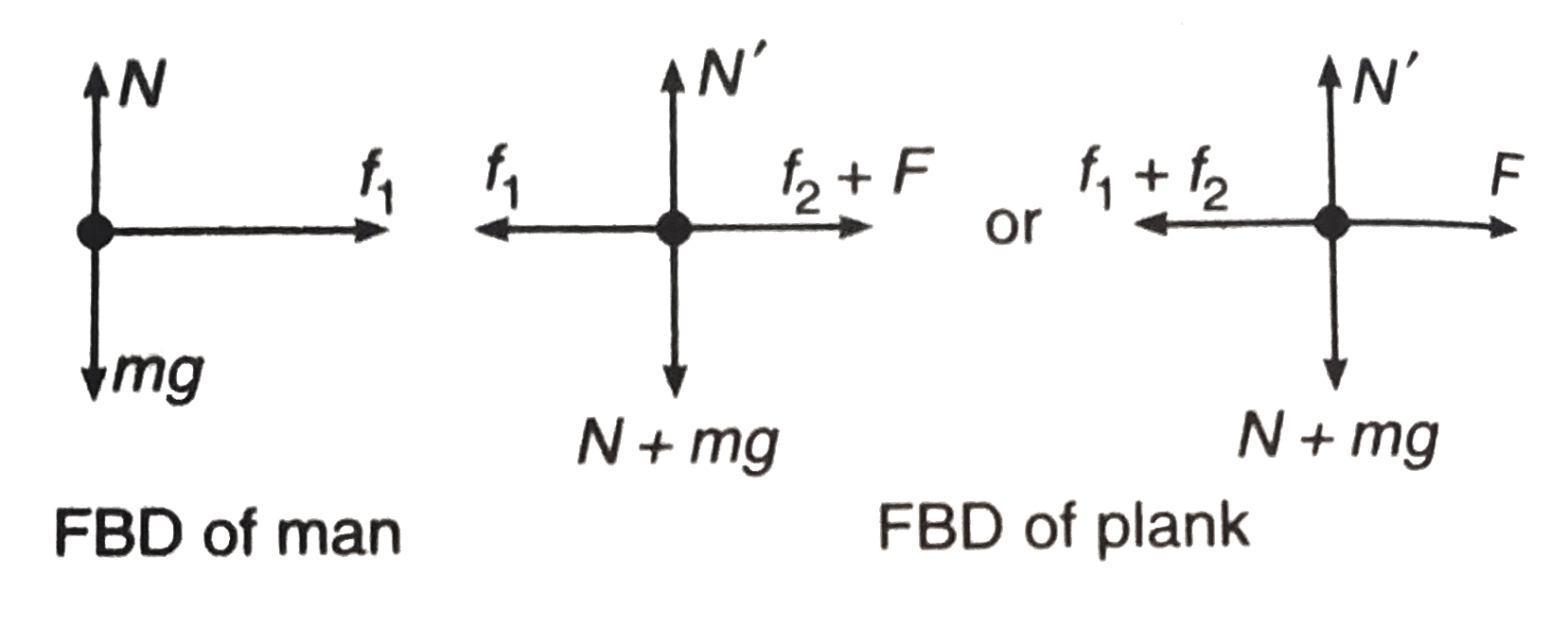
for the plank not to move
$F - {(f_{2})}_{max} \leq f_{1} \leq F + {(f_{2})}_{max}$
or $F - μ (M + m) g \leq m a \leq F + μ (M + m) g$
or a should lie between $\frac{F}{m} - \frac{μ (M + m) g}{m}$
and $\frac{F}{m} + \frac{μ (M + m) g}{m}$

Updated on:21/07/2023

A uniform plank of Young's modulus Y is moved over a smooth horizontal surface by a constant horizontal force F. The area of cross section of the plank is A. The compressive strain on the plank in the direction of the force is
A $F / A Y$
B $2 F / A Y$
C $\frac{1}{2} (F / A Y)$
D $3 F / A Y$
A plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is $μ = 0.5$ , the minimum acceleration of man so that plank does not slide is :

A $8 m / s^{2}$
B $4 m / s^{2}$
C $6 m / s^{2}$
D $3 m / s^{2}$
A plank of mass M is placed on a rough horizontal surface. A man m walks on the plank with an acceleration 'a' while the plank is also acted upon by a horizontal force F whose magnitude and direction can be adjusted to keep the plank at rest.

The coefficient of friction between plank and surface is $μ$ . Choose the correct options.
.
AThe maximum value of F to keep plank at rest is $m a + μ (M + m) g$
BThe minimum value of F to keep the plank at rest is $m a - μ (M + m) g$
CThe direction of friction on ground due to plank will always be forward
DIf $F = m a$ then friction on man due to plank is also F and friction between plank and ground will be zero