A point charge Q is placed at origin. Let →EA,→EB,and→EC be the electirc field at three points A (1,2,3), B (1,1,1), and C(2,2,2) due to charge Q. Then
→EA⊥→EB
→EA∣∣→EB
∣∣→EB∣∣=4∣∣→EC∣∣
→EB=16∣∣→EC∣∣
The correct Answer is:A, C
To solve the problem of finding the relationship between the electric fields at points A, B, and C due to a point charge Q placed at the origin, we will follow these steps:
Step 1: Define the position vectors
The position vectors of the points A, B, and C with respect to the origin (where the charge Q is located) are:
- Point A: →rA=^i+2^j+3^k
- Point B: →rB=^i+^j+^k
- Point C: →rC=2^i+2^j+2^k
Step 2: Calculate the magnitudes of the position vectors
Next, we calculate the magnitudes of these position vectors:
- Magnitude of →rA:
RA=|→rA|=√12+22+32=√1+4+9=√14
- Magnitude of →rB:
RB=|→rB|=√12+12+12=√1+1+1=√3
- Magnitude of →rC:
RC=|→rC|=√22+22+22=√4+4+4=√12
Step 3: Calculate the electric fields at points A, B, and C
The electric field →E due to a point charge Q at a distance R is given by:
→E=kQR2^r
where ^r is the unit vector in the direction of the position vector.
- Electric field at point A:
→EA=kQR2A^rA=kQ14→rA|→rA|=kQ14^i+2^j+3^k√14
- Electric field at point B:
→EB=kQR2B^rB=kQ3→rB|→rB|=kQ3^i+^j+^k√3
- Electric field at point C:
→EC=kQR2C^rC=kQ12→rC|→rC|=kQ122^i+2^j+2^k√12=kQ12^i+^j+^k√3
Step 4: Compare the magnitudes of the electric fields
Now we can compare the magnitudes of the electric fields:
- Magnitude of →EA:
|→EA|=kQ14√14
- Magnitude of →EB:
|→EB|=kQ3√3
- Magnitude of →EC:
|→EC|=kQ12√3
Step 5: Establish the relationship
To find the relationship between |→EB| and |→EC|:
|→EB|=kQ3√3,|→EC|=kQ12√3
From this, we can see that:
|→EB|=4⋅|→EC|
Conclusion
Thus, the electric field at point B is four times the electric field at point C:
→EB=4⋅→EC
The position vectors of the points A, B, and C with respect to the origin (where the charge Q is located) are:
- Point A: →rA=^i+2^j+3^k
- Point B: →rB=^i+^j+^k
- Point C: →rC=2^i+2^j+2^k
Next, we calculate the magnitudes of these position vectors:
- Magnitude of →rA:
RA=|→rA|=√12+22+32=√1+4+9=√14
RB=|→rB|=√12+12+12=√1+1+1=√3
RC=|→rC|=√22+22+22=√4+4+4=√12
The electric field →E due to a point charge Q at a distance R is given by:
→E=kQR2^r
where ^r is the unit vector in the direction of the position vector.
→EA=kQR2A^rA=kQ14→rA|→rA|=kQ14^i+2^j+3^k√14
→EB=kQR2B^rB=kQ3→rB|→rB|=kQ3^i+^j+^k√3
→EC=kQR2C^rC=kQ12→rC|→rC|=kQ122^i+2^j+2^k√12=kQ12^i+^j+^k√3
Now we can compare the magnitudes of the electric fields:
- Magnitude of →EA:
|→EA|=kQ14√14
|→EB|=kQ3√3
|→EC|=kQ12√3
To find the relationship between |→EB| and |→EC|:
|→EB|=kQ3√3,|→EC|=kQ12√3
From this, we can see that:
|→EB|=4⋅|→EC|
Thus, the electric field at point B is four times the electric field at point C:
→EB=4⋅→EC
Similar Questions
A point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionThree large identical conducting parallel plates carrying charge +Q,−Q,and+2Q, respectively, are placed as shown in figure. If EA,Eb,andEC refer to the magnitudes of the electric field at points A, B, and C, respectively. Then
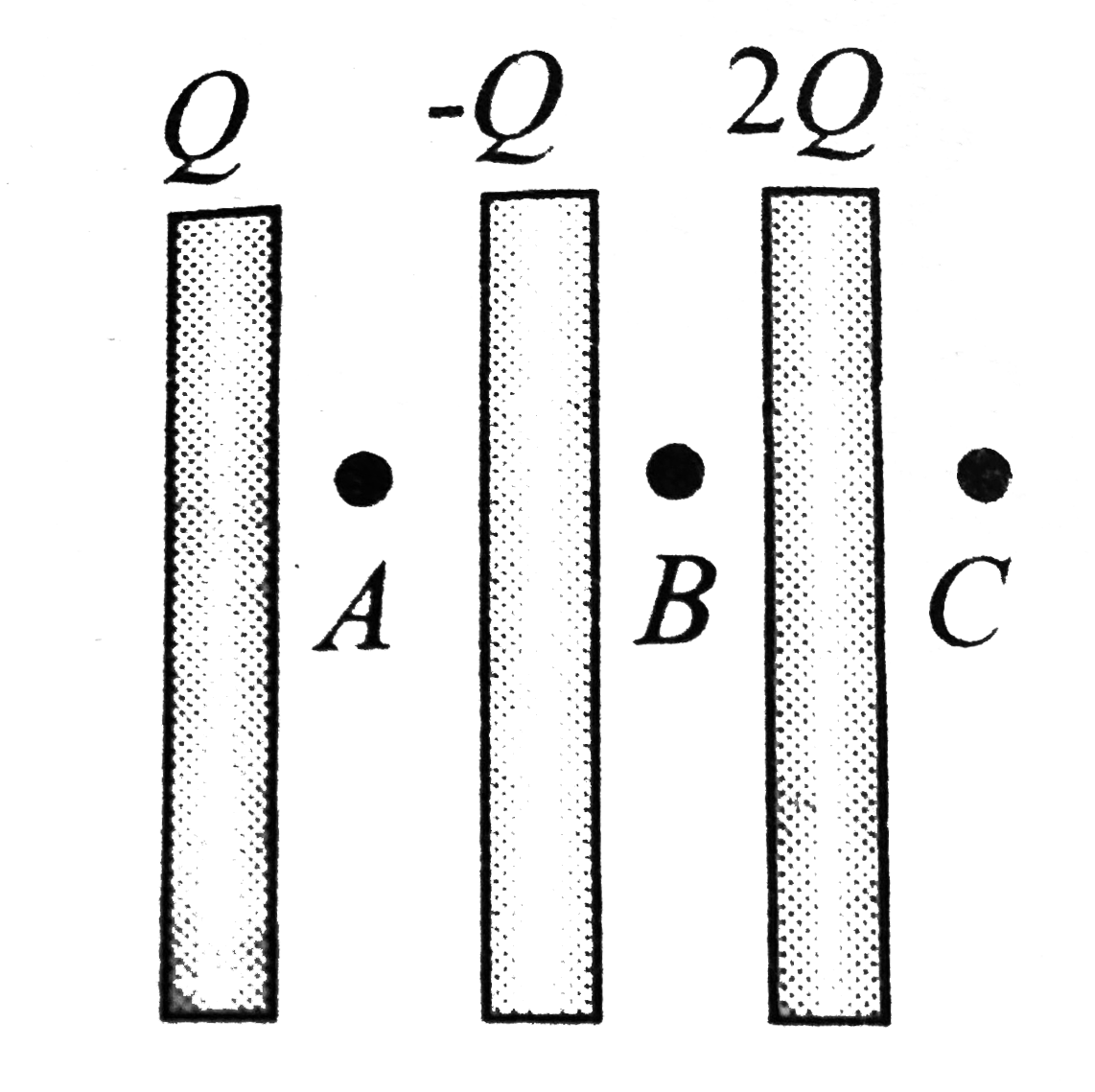 View Solution
View SolutionIdentify A and B:
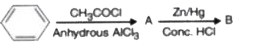 View Solution
View SolutionA Gaussian surface S encloses two charges q1=qandq2=−qthe field at p is
where →E1,→E2and→E3 are the field contributed by q1,q2andq3at P respectively.
 View Solution
View SolutionA charge Q located at a point →r is in equilibrium under the combined field of three charges q1,q2 and q3. If the charges q1 and q2 are located at point →r1 and →r2 respectively, find the direction of the force on Q due to q3 in terms of q1,(q2),→r1→r2, and →r.
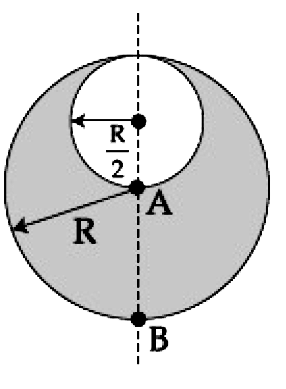
View SolutionConsider a sphere of radius R which carries a uniform charge density ρ. If a sphere of radius R2 is carved out of it,as shown, the ratio →EA→EB of magnitude of electric field →Ea and →EB, respectively, at points A and B due to the remaining portion is:
 View Solution
View SolutionA charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
View SolutionThe point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
View SolutionFigure shows a conducting sphere with a cavity. A point charge q1 is placed inside cavity, and q2 is placed out side the sphere →Ein is electric field due to charge induced on surface of cavity. →Eout is electric field due to charge induced on outer surface of sphere and →Enet is net field at any point. Two closed gaussian surface S1 & S2 are also drawn in the figure.
 View Solution
View SolutionA point charge qA=+100μc is placed at point A (1, 0, 2) m and another point charge qB=+200μc is placed at point B (4, 4, 2) m. Find :
(i) Magnitude of electrostatic interaction force acting between them
(ii) Find →FA (force on A due to B) and →FB (force on due to A) in vector formView Solution
