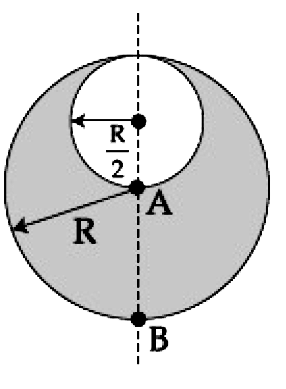
Consider a sphere of radius R which carries a uniform charge density ρ. If a sphere of radius R2 is carved out of it,as shown, the ratio →EA→EB of magnitude of electric field →Ea and →EB, respectively, at points A and B due to the remaining portion is:
Option1 2134
Option2 1734
Option3 1834
Option4 1854
Step by step video & image solution for Consider a sphere of radius R which carries a uniform charge density rho. If a sphere of radius R/2 is carved out of it,as shown, the ratio (vecE_(A))/(vecE_(B)) of magnitude of electric field vecE_(a) and vecE_(B), respectively, at points A and B due to the remaining portion is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
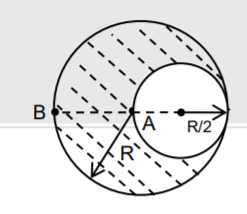
A solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

View SolutionA positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?

View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
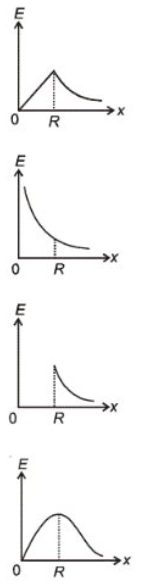
View SolutionA non-conducting solid sphere of radius R, has a uniform charge density. The graph representing variation of magnitude of electric field (E) as a function of distance (x) from the centre of the sphere is
View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
View Solution
