A point source of sound is moving uniformly along positive x direction with velocity V0. At time t=0 the source was at origin and emitted a compression pulse C1. After time T it emitted another compression pulse C2. Write the equation of the wave front representing the compression pulse C2 at time t(>T). Speed of sound is V.
The correct Answer is:(x−V0T)2+y2+z2=V2(t−T)2
Step by step video, text & image solution for A point source of sound is moving uniformly along positive x direction with velocity V_(0). At time t = 0 the source was at origin and emitted a compression pulse C_(1). After time T it emitted another compression pulse C_(2). Write the equation of the wave front representing the compression pulse C_(2) at time t (gt T). Speed of sound is V. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle of mass m is moving with constant velocity v0 along the line y=b. At time t=0 it was at the point (0,b). At time t=bv0, the

View SolutionA wave propagates on a string in the positive x-direction at a velocity u. The shape of the string at t=t0 is given by g(x,t0)=Asin(xa) . Write the wave equation for a general time t.
View Solution
Knowledge Check
A particle is moving with speed v=b√x along positive x-axis. Calculate the speed of the particle at time t=τ (assume that the particle is at origin at t = 0).
Ab2τ√2Bb2τ4Cb2τ2Db2τA pulse travelling at a speed of 2ms along the positive Z-axis is given by y =3z2+1 at t= 0 .The wave function representing the pulse at any times is given by
Ay=3(z−2t)2+1By=3(z+2t)2+1Cy=3(2z+t)2+1Dy=3(2z−t)2+1The velocity (v) - time (t) graph for a particle moving along x - axis is shown in the figure. The corresponding position (x) - time (t) is best represented by
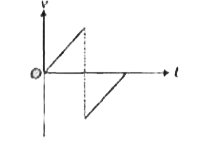 A
A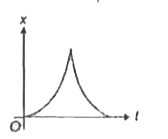 B
B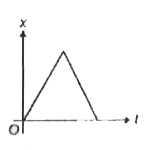 C
C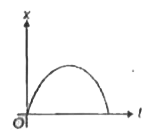 D
D
If at t=0, a travelling wave pulse on a string is described by the function.
y=6x2+3
What will be the waves function representing the pulse at time t, if the pulse is propagating along positive x-axis with speed 4m/s?
View SolutionA particle located at "x=0" at time "t=0" starts moving along the positive "x" - direction with a velocity "v" that varies as "v=alpha sqrt(x)".The displacement "(x)" of the particle varies with time as "(alpha" is constant)
View SolutionA particle located at x=0 at time t=0, starts moving along with the positive x−direction with a velocity 'v' that varies as v=a√x. The displacement of the particle varies with time as
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given by
View SolutionIf at t=0, a travelling wave pulse on a string is described by the function.
y=6x2+3
What will be the waves function representing the pulse at time t, if the pulse is propagating along positive x-axis with speed 4m/s?
View Solution
