A projectile rises to a height of 10 m and then falls at a distance of 30 m away from the projection. Its vertical displacement is
0 m
5 m
6 m
7 m
The correct Answer is:A
To solve the problem, we need to determine the vertical displacement of the projectile that rises to a height of 10 m and then falls to a distance of 30 m away from the projection point.
1. Understanding Vertical Displacement:
- Vertical displacement is defined as the difference in the vertical position of an object from its initial position to its final position.
2. Initial Position:
- The projectile is launched from the ground level, which we can consider as the initial vertical position (0 m).
3. Maximum Height:
- The projectile reaches a maximum height of 10 m during its flight. However, this is not the final position.
4. Final Position:
- After reaching the maximum height, the projectile falls back down. Since it is stated that it falls at a distance of 30 m away from the projection point, it lands back on the ground.
5. Calculating Vertical Displacement:
- The final vertical position of the projectile when it lands is also 0 m (ground level).
- Therefore, the vertical displacement can be calculated as:
Vertical Displacement=Final Position−Initial Position=0m−0m=0m
6. Conclusion:
- The vertical displacement of the projectile is 0 m.
Final Answer:
The vertical displacement is 0 m.
---
- Vertical displacement is defined as the difference in the vertical position of an object from its initial position to its final position.
- The projectile is launched from the ground level, which we can consider as the initial vertical position (0 m).
- The projectile reaches a maximum height of 10 m during its flight. However, this is not the final position.
- After reaching the maximum height, the projectile falls back down. Since it is stated that it falls at a distance of 30 m away from the projection point, it lands back on the ground.
- The final vertical position of the projectile when it lands is also 0 m (ground level).
- Therefore, the vertical displacement can be calculated as:
Vertical Displacement=Final Position−Initial Position=0m−0m=0m
- The vertical displacement of the projectile is 0 m.
The vertical displacement is 0 m.
Topper's Solved these Questions
- KINEMATICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - KINEMATICSEXERCISE - Numericals
26 Videos
- GRAVITATIONBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - GRAVITATIONEXERCISE - MULTIPLE CHOICE QUESTIONS
19 Videos
- KINETIC THEORY OF GASESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective question
20 Videos
Similar Questions
A projectile has a range of 40 m and reaches a maximum height of 10 m. Find the angle at which the projectile is fired.
View SolutionA projectile of mass 3m is projected from ground with velocity 20√2m/s at 45∘. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of 100m from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
(g=10m/s2)
View Solution
Knowledge Check
A ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.Bits velocity decreases and acceleration increases.Cits velocity increases and acceleration remains constant.Dits velocity and acceleration remains constant.A ball is thrown from the ground so as to just clear a wall 10m high at a distance of 20m and falls at a distance of 40m from the wall. The magnitude and direction of the projection velocity is
A10m/s,30∘B25m/s,60∘C25m/s,tan−1(3/4)D10m/s,tan−1(3/4)A steel ball of mass 0.1 kg falls freely from a height of 10 m and bounces to a height of 5.4 m from the ground. If the dissipated energy in this process is absorbed by the ball, the rise in its temperature is (specific heat of steel =460K/kg∘/C,g=10m/s2)
A0.01∘CB0.1∘CC1∘CD1.1∘C
A projectile thrown from a height of 10 m with velocity of √2m/s the projectile will fall, from the foot of projection, at distance- (g=10m/s2)
View SolutionA ball is projected from ground with a speed of 20ms−1 at an angle of 45∘ with horizontal.There is a wall of 25m height at a distance of 10m from the projection point. The ball will hit the wall at a height of
View SolutionA body has a free fall from a height of 20 m. After falling through a distance of 5 m, the body would
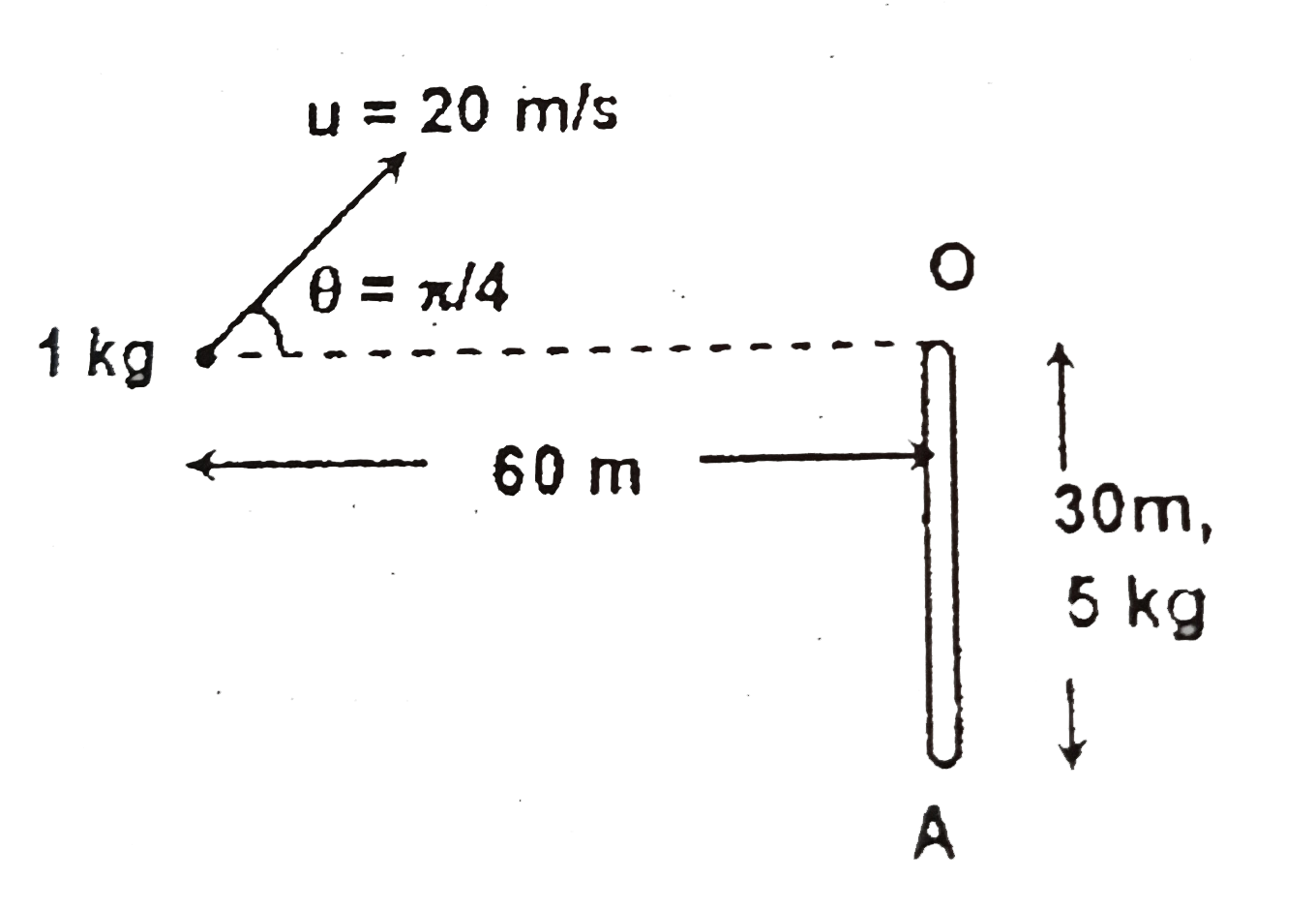
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If projectile is fired horizontally, it will
View SolutionA projectile has a range of 40m and reaches a maximum height of 10m. Find the angle at which the projectile is fired.
View Solution
