A radioactive sample has N0 active at t=0 . If the rate of disintegration at any time is R and the number of atoms is N, them the ratio R/N varies with time as.
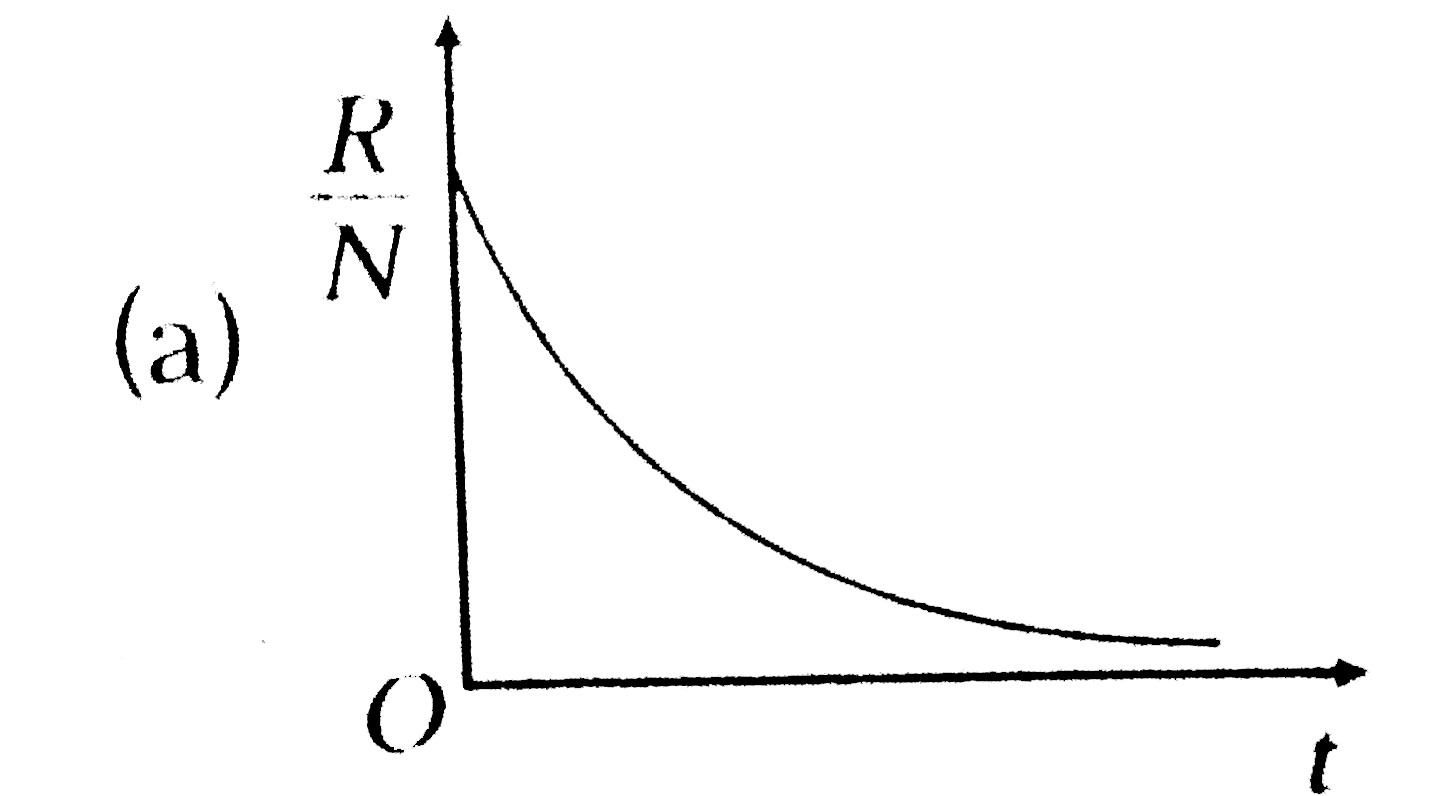

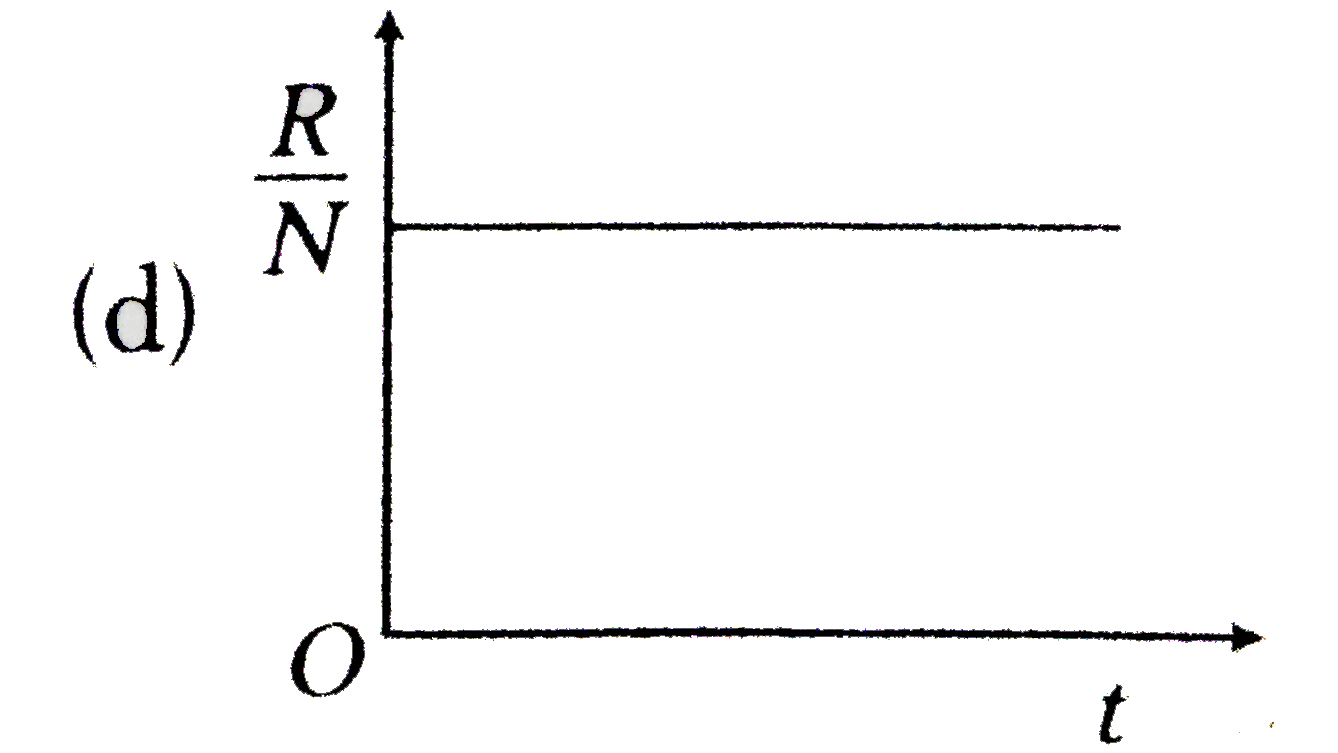
The correct Answer is:D
To solve the problem step by step, we need to analyze the relationship between the rate of disintegration R and the number of radioactive atoms N over time.
Step 1: Understand the relationship between R and N
The rate of disintegration R is defined as the number of disintegrations per unit time. According to the principles of radioactive decay, the rate of disintegration can be expressed as:
R=−dNdt
This equation states that the rate of disintegration is equal to the negative rate of change of the number of atoms N.
Step 2: Express N in terms of time
The number of radioactive atoms N at any time t can be expressed using the exponential decay formula:
N(t)=N0e−λt
where N0 is the initial number of atoms at t=0 and λ is the decay constant.
Step 3: Differentiate N(t) to find R
To find the rate of disintegration R, we differentiate N(t):
R=−dNdt=−ddt(N0e−λt)=N0λe−λt
Step 4: Find the ratio RN
Now, we can find the ratio RN:
RN=N0λe−λtN0e−λt=λ
This shows that the ratio RN is equal to the decay constant λ.
Step 5: Analyze the result
Since λ is a constant, we conclude that the ratio RN does not vary with time. It remains constant as time progresses.
Final Answer
Thus, the ratio RN varies with time as a constant value λ.
---
The rate of disintegration R is defined as the number of disintegrations per unit time. According to the principles of radioactive decay, the rate of disintegration can be expressed as:
R=−dNdt
This equation states that the rate of disintegration is equal to the negative rate of change of the number of atoms N.
The number of radioactive atoms N at any time t can be expressed using the exponential decay formula:
N(t)=N0e−λt
where N0 is the initial number of atoms at t=0 and λ is the decay constant.
To find the rate of disintegration R, we differentiate N(t):
R=−dNdt=−ddt(N0e−λt)=N0λe−λt
Now, we can find the ratio RN:
RN=N0λe−λtN0e−λt=λ
This shows that the ratio RN is equal to the decay constant λ.
Since λ is a constant, we conclude that the ratio RN does not vary with time. It remains constant as time progresses.
Thus, the ratio RN varies with time as a constant value λ.
Topper's Solved these Questions
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - B Medical entrance special format questions
9 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - MATCH THE COLUMNS
4 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - CHECK POINT 13.3
15 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
Similar Questions
The rate of disintegration of a radioactive substance is …………………………… to the number of atoms present at that time .
View SolutionThe radioactive of a sample is R1 at a time T1 and R2 at a time T2. If the half-life of the specimen is T, the number of atoms that have disintegrated in the time (T2−T1) is equal ton(R1−R2)Tln4. Here n is some integral number. What is the value of n?
View Solution
Knowledge Check
The activity of a radioactive sample is measures as N0 counts per minute at t=0 and N0/e counts per minute at t=5min. The time (in minute) at which the activity reduces to half its value is.
Aloge25B5loge2C5log102D5loge2
The radioactivity of a sample is R1 at a time T1 and R2 at time T2. If the half-life of the specimen is T, the number of atoms that have disintegrated in the time (T2−T1) is proporational to
View SolutionA radioactive sample has initial concentration N0 of nuclei. Then,
View SolutionThe activity of a radioactive sample is measures as N0 counts per minute at t=0 and N0/e counts per minute at t=5min. The time (in minute) at which the activity reduces to half its value is.
View SolutionHalf-life of a radioactive substance is T. At time t_1 activity of a radioactive substance is R1 and at time t2 it is R2. Find the number of nuclei decayed in this interval of time.
View SolutionIn a radioactive disintegration, the ratio of initial number of atoms to the number of atoms present at an instant of time equal to its mean life is
View SolutionA radioactive sample has a mass m, decay cosntant λ, and molecular weight M. If the Avogadro number is NA, then
(a) find the initial number of neclei present, (b) find the number of deacyed nuceli after a time t, (c ) find the activity of the sample after a time t,
View SolutionA parent radioactive nucleus A (decay constant λA) converts into a radio-active nucleus B of decay constant λb, initially, number of atoms of B is zero At any time Na,Nb are number of atoms of nuclei A and B respectively then maximum velue of Nb.
View Solution
