A ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
tan−1(2/3)
sin−1(2/3)
90∘
cos−1(1/3)
The correct Answer is:C
To solve the problem, we need to determine the angle of incidence (I) such that a ray of light entering a glass sphere with a refractive index (n) of 3/2 does not emerge from the sphere. This involves understanding the concept of total internal reflection (TIR).
1. Understanding the Critical Angle:
The critical angle (θ_c) is the angle of incidence above which total internal reflection occurs. It can be calculated using the formula:
sin(θc)=1n
where n is the refractive index of the material.
2. Calculate the Critical Angle:
Given that the refractive index n=32:
sin(θc)=132=23
Now, we can find θc using the inverse sine function:
θc=sin−1(23)
3. Condition for Total Internal Reflection:
For the ray to not emerge from the sphere, the angle of incidence (I) at the point of incidence on the sphere must be greater than the critical angle:
I>θc
4. Finding the Angle of Incidence:
Since the maximum angle of incidence that can be used to ensure TIR is when I=90∘, we can conclude that if the angle of incidence is 90∘, the ray will not exit the sphere.
5. Conclusion:
Therefore, the angle of incidence (I) should be 90∘ to ensure that the ray does not come out of the sphere.
Final Answer:
The angle of incidence should be 90∘.
---
The critical angle (θ_c) is the angle of incidence above which total internal reflection occurs. It can be calculated using the formula:
sin(θc)=1n
where n is the refractive index of the material.
Given that the refractive index n=32:
sin(θc)=132=23
Now, we can find θc using the inverse sine function:
θc=sin−1(23)
For the ray to not emerge from the sphere, the angle of incidence (I) at the point of incidence on the sphere must be greater than the critical angle:
I>θc
Since the maximum angle of incidence that can be used to ensure TIR is when I=90∘, we can conclude that if the angle of incidence is 90∘, the ray will not exit the sphere.
Therefore, the angle of incidence (I) should be 90∘ to ensure that the ray does not come out of the sphere.
The angle of incidence should be 90∘.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
A horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionUnpolarized light is incident on a plane glass surface. What should be the angle of incidence so that the reflected and refracted rays are perpendicular to eachother ?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light is incident on the left vertical face of glass cube of refractive index n2, as shown in figure. The plane of incidence is the plane of the page, and the cube is surrounded by liquid (refractive index=n1). What is the largest angle of incidence θ1 for which total internal reflection occurs at the top surfaces?

View SolutionUnpolarized light is incident on a plane glass surface having refractive index . The angle of incidence at which reflected and refracted rays would become perpendicular to each other is :
View SolutionA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
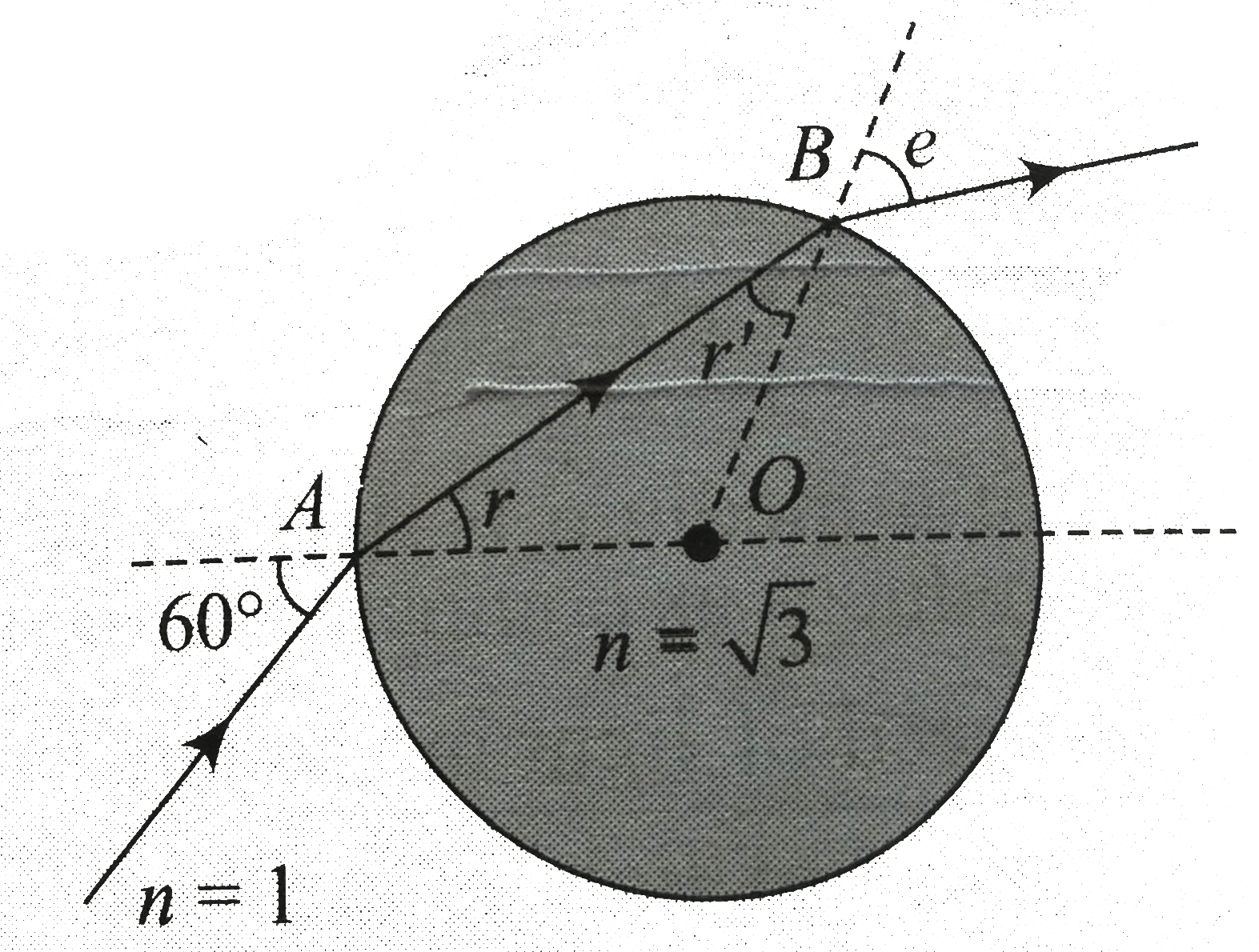
View SolutionA ray of light enters a rectangular glass slab of refractive index √3 at an angle of incidence 60∘. It travels a distance of 5cm inside the slab and emerges out of the slab. The perpendicular distance between the incident and the emergent rays is
View Solution
