A rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is μ. Let the mass of the box be m .
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to α>θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?
Consider the adjacent diagram , force of friction on the box will act up the plane .
For the box to just starts sliding down mg
sin θ=f=μN=μmg cos θ
or tanθ=μ⇒θ=tan−1(μ)
(b) When angle of inclination is increased to α<θ , then
net force acting on the box , down the plane is
F1= mg sinα−f=mg sin α−μN
= mg (sin α−μcosα)
(c) To keep the box either stationary or just move it up with uniform speed , upward force needed , F2=mg sinα+f=mg(sinα+μcosα) (In this case , friction would act down the plane .)
(d) In the box is to be moved with an upward acceleration a , then upward force needed , F3=mg(sinα+μcosα)+ ma.
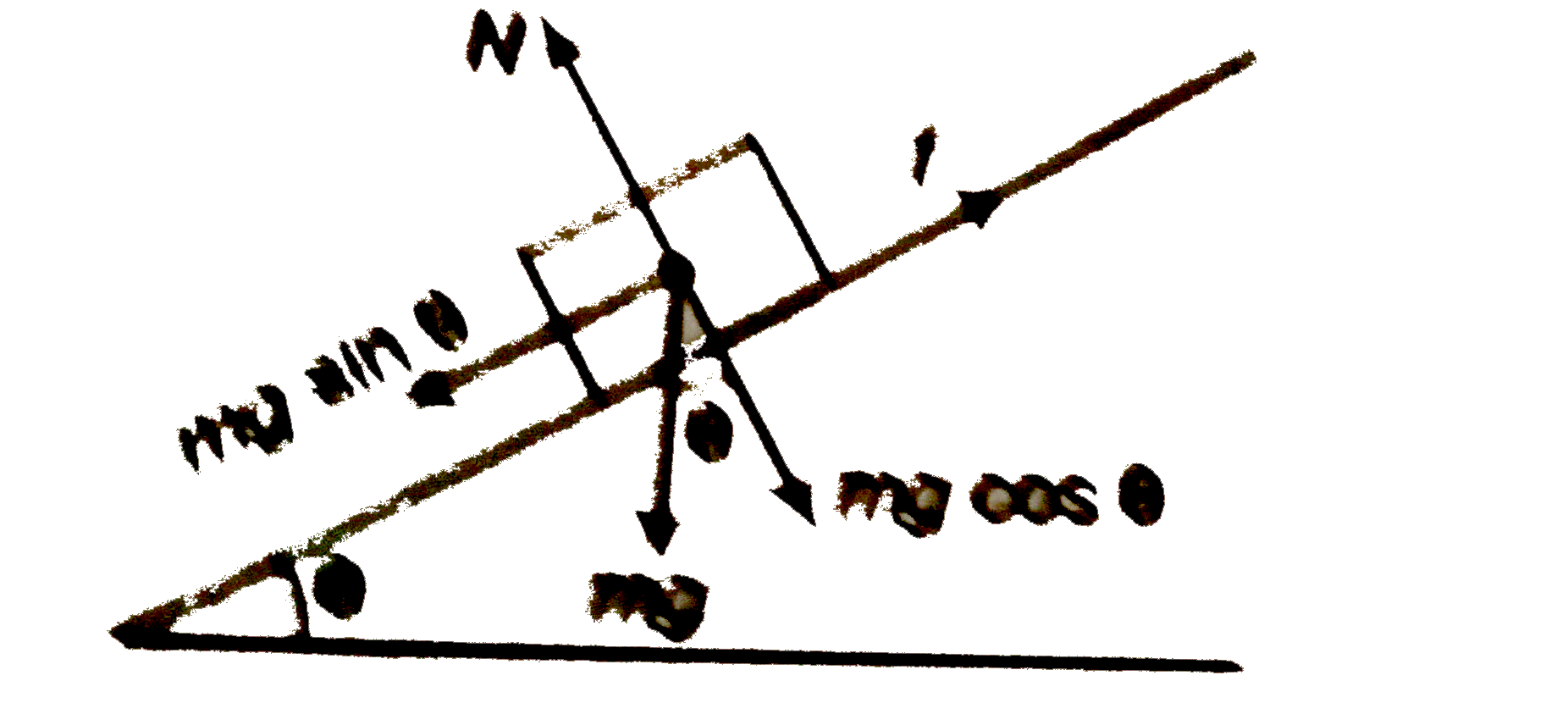
Topper's Solved these Questions
- LAWS OF MOTIONBook:NCERT EXEMPLAR ENGLISHChapter:LAWS OF MOTIONExercise:Short answer type questions
Explore 6 Videos
- KINETIC THEORYBook:NCERT EXEMPLAR ENGLISHChapter:KINETIC THEORYExercise:Multiple Choice Questions (MCQs)
Explore 31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT EXEMPLAR ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Long Answer Type Questions
Explore 3 Videos
Similar Questions
A block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

View SolutionA body is sliding down an inclined plane having coefficient of friction 0.5. If the normal reaction is twice that of the resultant downward force along the inclination the angle between the inclined plane and the horizontal is
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
The angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA body is sliding down an inclined plane having coefficient of friction 1/3. If the normal reaction is three times that of the resultant downward force along the incline, the angle between the inclined plane and the horizontal is
View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionA body takes ''n'' times as much time to slide down a rough inclined plane as it takes to slide down an identical but smooth inclined plane. If the angle of inclination of the inclined plane is ''θ''. What is the coefficient of friction between the body and the rough plane ?
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionThe force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is 60∘ is .
View Solution