A rectangular metallic loop of length l and width b is placed coplanerly with a long wire carrying a current I . The loop is moved perpendicular to the wire with a speed v in the plane containing the wire and the loop. Calculate the emf induced in the loop when the rear end of hte loop is at a distance a from the wire. Solve by unsing Faraday's law for the flux thrugh the loop and also by replacing different sagments with equivalent batteries.
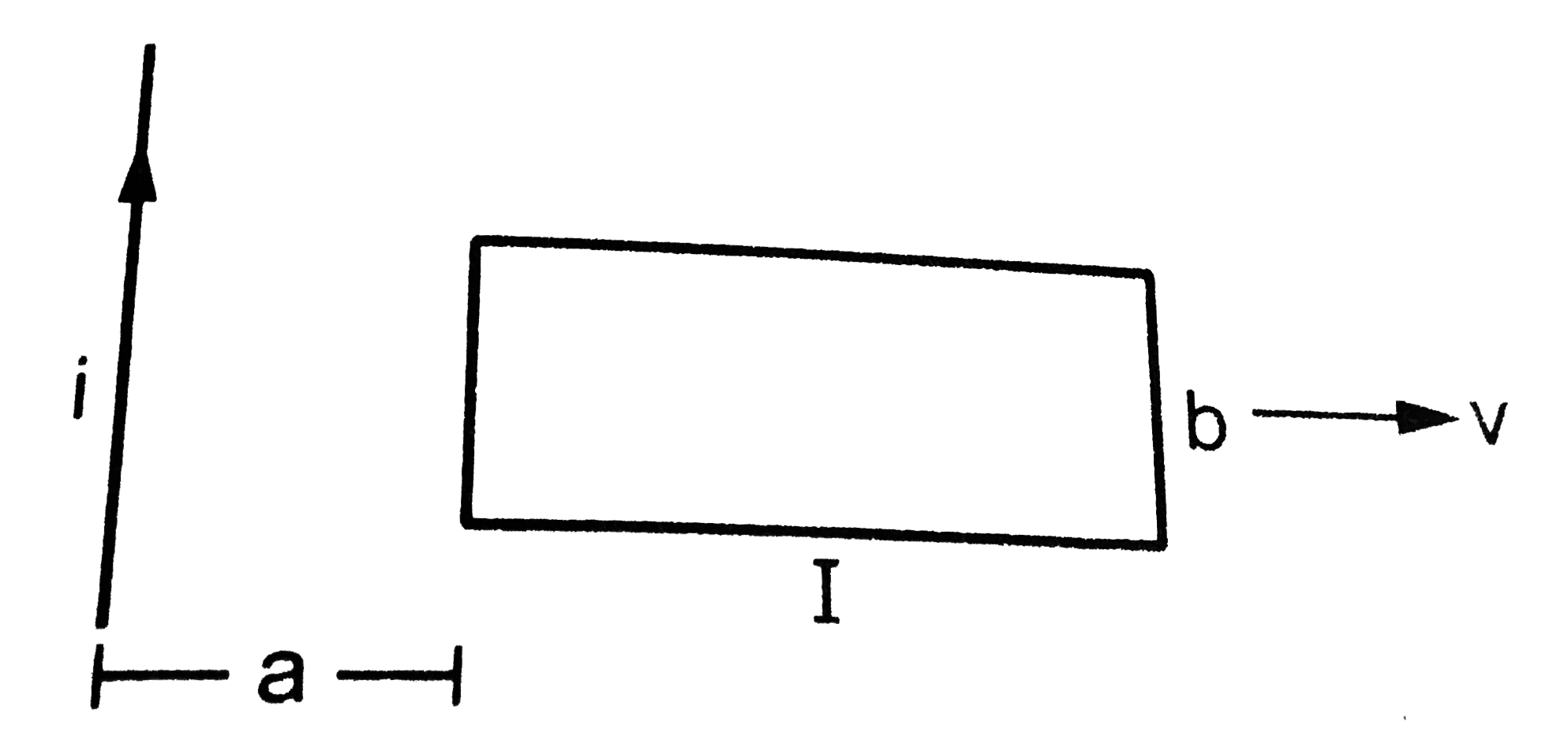
(a) Using Faraday's law<br>Cosider a unit length dx at a distance x <br>B=(mu_0i)/(2 pi x) Area of strip =bdx<br>d phi = (mu_0i)/(2 pi x) bdx<br> implies phi= int^(a+l)_(a) (mu_0 i)/(2 pi x) bdx<br>=(mu_0 i)/(2 pi)b int_(a)^(a+l)((dx)/(x))<br>=(mu_0 i)/(2 pi x) log ((a+l)/(a))<br>Emf= (d phi)/(dt)=d/(dt)[(mu_0 i)/(2 pi) log ((a+l)/(a))]<br>=(mu_0 i)/(2 pi)((a)/(a+l)) ((va-(a+l)v)/(a^2))<br>(where (da)/(dt)=v)<br>= (mu_0ib)/(2 pi) (a)/(a+l) (vl)/(a^2)<br>=μ0ibvl2π(a+l)a
the velocities of AB and CD create e.m/f because the emf 's due to to AD and BC are equal and opposite to each other.
∴BAB=μ0i2πa
Emf_(AB)=(mu_0i)/(2 pi a)<br>length =b, velocity =v <br>B_(CD)=(mu_0i)/(2 pi(a+l))<br>Emf'_(CD)=(mu_0ibv)/(2 pi(a+l))<br>Net E.m.f.=(mu_0ibv)/(2 pi a))-(mu_0ibv)/(2 pi(a+l))<br>=(mu_0ibvl (a+l)- mu ib va)/(2 pi a(a+l))<br>(mu_0ibvl)/(2 pi(a+l)).
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
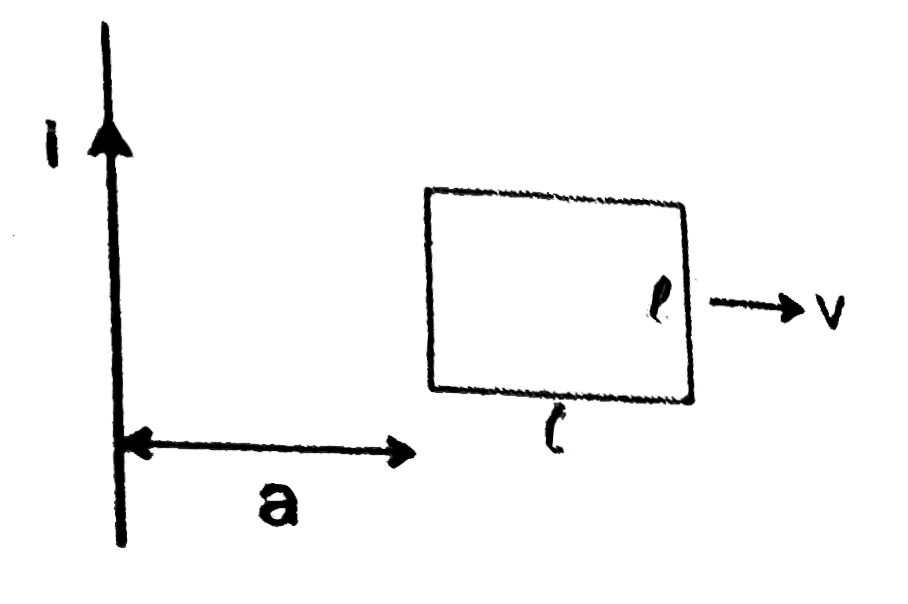
A square metallic loop of side l is placed near a fixed long wire carrying a current i(figure).The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop.The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ.Find out value of x.
View SolutionA square metallic loop of side l is placed near a fixed long wire carrying a current i(figure).The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop.The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ.Find out value of x.
View Solution
Knowledge Check
- Question 1 - Select One
A rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
Aμ0i4π8√a2+b2abBμ0i4π4√a2+b2abCμ0i4π2√a2+b2abDμ0i4π√a2+b2ab - Question 2 - Select One or More
A long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
Amoved parallel to the wireBroatated about an axis perpendicular to the plane of the loop passing through the centre of the loopCrotated about an axis parallel to the wire passing through the centre of the loopDmoved away from the wire
A square meallic loop of side l is placed near a fixed long wire carrying a current i (figure). The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop. The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ. Find out value of x .
View SolutionA rectangular loop of wire shown below is coplanar with a long wire carrying current I.
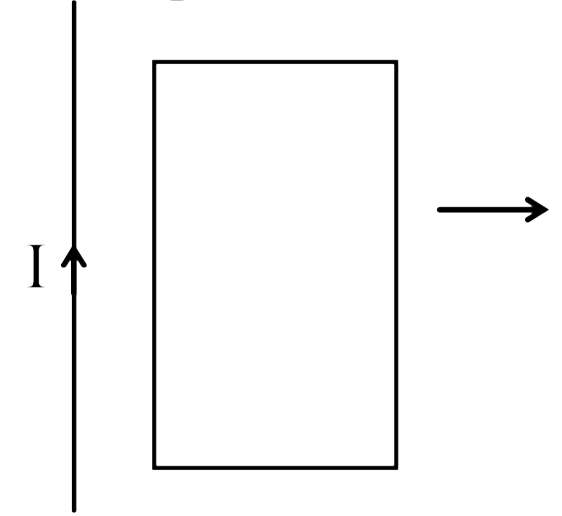The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and the right sides of the loop View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
View Solution