An inductor of inducance 5.0 H, having a negligible resistance, is connected in series with a 100Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the given values
- Inductance (L) = 5.0 H
- Resistance (R) = 100 Ω
- EMF of the battery (E₀) = 2.0 V
- Time (t) = 20 ms = 20 × 10⁻³ s
Step 2: Calculate the time constant (τ)
The time constant (τ) for an RL circuit is given by the formula:
τ=LR
Substituting the values:
τ=5.0H100Ω=0.05s=50ms
Step 3: Calculate the maximum current (I₀)
The maximum current (I₀) in the circuit can be calculated using:
I0=E0R
Substituting the values:
I0=2.0V100Ω=0.02A=20mA
Step 4: Calculate the current (I) at time t
The current (I) at any time t in an RL circuit is given by:
I=I0(1−e−tτ)
Substituting the values:
I=0.02(1−e−20×10−30.05)
Calculating the exponent:
−20×10−30.05=−0.4
So,
I=0.02(1−e−0.4)
Using the value of e−0.4≈0.6703:
I=0.02(1−0.6703)=0.02×0.3297≈0.006594A≈6.59mA
Step 5: Calculate the potential difference across the resistor (Vᵣ)
The potential difference across the resistor can be calculated using Ohm's law:
Vr=I×R
Substituting the values:
Vr=0.006594A×100Ω≈0.6594V≈0.66V
Final Answer
The potential difference across the resistor 20 ms after the circuit is switched on is approximately 0.66 V.
---
- Inductance (L) = 5.0 H
- Resistance (R) = 100 Ω
- EMF of the battery (E₀) = 2.0 V
- Time (t) = 20 ms = 20 × 10⁻³ s
The time constant (τ) for an RL circuit is given by the formula:
τ=LR
Substituting the values:
τ=5.0H100Ω=0.05s=50ms
The maximum current (I₀) in the circuit can be calculated using:
I0=E0R
Substituting the values:
I0=2.0V100Ω=0.02A=20mA
The current (I) at any time t in an RL circuit is given by:
I=I0(1−e−tτ)
Substituting the values:
I=0.02(1−e−20×10−30.05)
Calculating the exponent:
−20×10−30.05=−0.4
So,
I=0.02(1−e−0.4)
Using the value of e−0.4≈0.6703:
I=0.02(1−0.6703)=0.02×0.3297≈0.006594A≈6.59mA
The potential difference across the resistor can be calculated using Ohm's law:
Vr=I×R
Substituting the values:
Vr=0.006594A×100Ω≈0.6594V≈0.66V
The potential difference across the resistor 20 ms after the circuit is switched on is approximately 0.66 V.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
A coil of inductance 1.0 H and resistance 100 Omega is connected to a battery of emf 12 V. Find the energy stored in the magnetic field associated with the coil at an instant 10 ms after the circuit is switched on.
View SolutionA circuit containing five resistors is connected to a battery with a 12 v emf as shown in figure. The potential difference across 4Ω resistor is

View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the current in the circuit,
View SolutionAn LR circuit constains an inductor of 500 mH, a resistor of 25.OΩ and an emf of 5.00 V in series. Find the potential difference across the resistor at t =(a) 20.0 ms, (b) 100 ms and ( c) 1.00 s.
View SolutionA 50 mH inductor is in series with a 10 ohm resistor and a battery with an emf of 25 V. At t = 0 the switch is closed. Find
the power dissipated in the resistor
View SolutionThree resistors are connected to a 6 V battery as shown in the figure
Calculate:
potential difference across the 7.2 ohm resistor
View SolutionAn inductor-coil of inductance 20 mH having resistance 10Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at t=0, (b) t = 10 ms and (c ) t = 1.0s.
View SolutionAn inductor-coil of inductance 20 mH having resistance 10Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at t=0, (b) t = 10 ms and (c ) t = 1.0s.
View SolutionThree resistors are connected to a 6 V battery as shown in the figure given below :
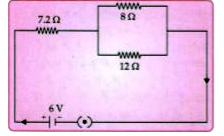
Calculate :
potential difference across the 7.2Ω resistor.
View SolutionA 10 V storage battery of negligible internal resistance is connected across a 50Ω resistor. How much heat energy is produced in the resistor in 1 hour
View Solution
