A rectangular tube of uniform cross section has three liquids of densities ρ1,ρ2 and ρ3. Each liquid column has length l equal to length of sides of the equilateral triangle. Find the length x of the liquid of density ρ1 in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

The correct Answer is:x=(ρ2−ρ1l2ρ2=(ρ1+ρ3)
Let us consider two points 1 and 2 in the horizontal limb. Pressure at 1 is P1 and ρ1gh1+ρ2gh2
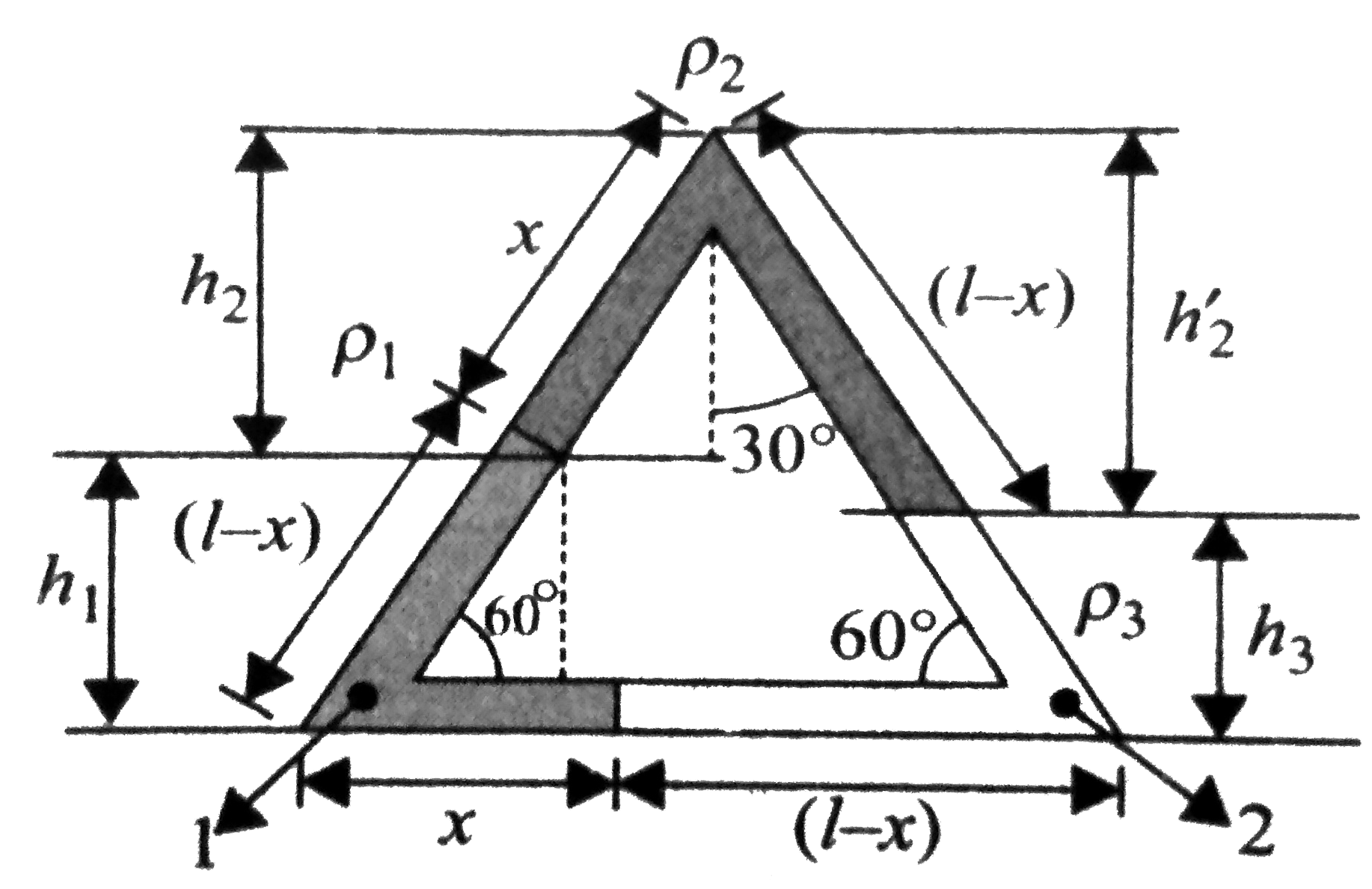
pressure at 2 is P2=ρgh′2=ρ3gh3
Since P1=P2 for non accelerating liquid, we have
ρ1h1+ρ2h2=ρ2h′2+ρ3h3
Substituting h1=h′2(l−x)sin60∘ and h2−h3=xsin60∘, we have
x=(ρ2−ρ1)l2ρ2−(ρ1+ρ3)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

View SolutionWhen a capillary tube of radius r is immersed in a liquid of density ρ, the liquid rises to a height h in it. If m is the mass of the liquid in the capillary tube, find the potential energy of this mass of the liquid in the tube.
View Solution
Knowledge Check
Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
Aπ2<θ1<θ2<θ3<πBπ>θ1>θ2>θ3>π2Cπ2>θ1>θ2>θ3≥0D0≤θ1<θ2<θ3<π2Three liquids having densities ρ1,ρ2,ρ3 are filled in a U-tube. Length of each liquid column is equal to I, ρ1>ρ2>ρ3 and liquids remain at rest (relative to the tube) in the position shown in the figure. It is possible that
 AU-tube is accelerating leftwardsBU-tube is accelerating upwards with acceleration gCU−tube is moving with a constant velocityDnone of the above
AU-tube is accelerating leftwardsBU-tube is accelerating upwards with acceleration gCU−tube is moving with a constant velocityDnone of the aboveA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
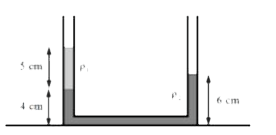 A13B25C12D45
A13B25C12D45
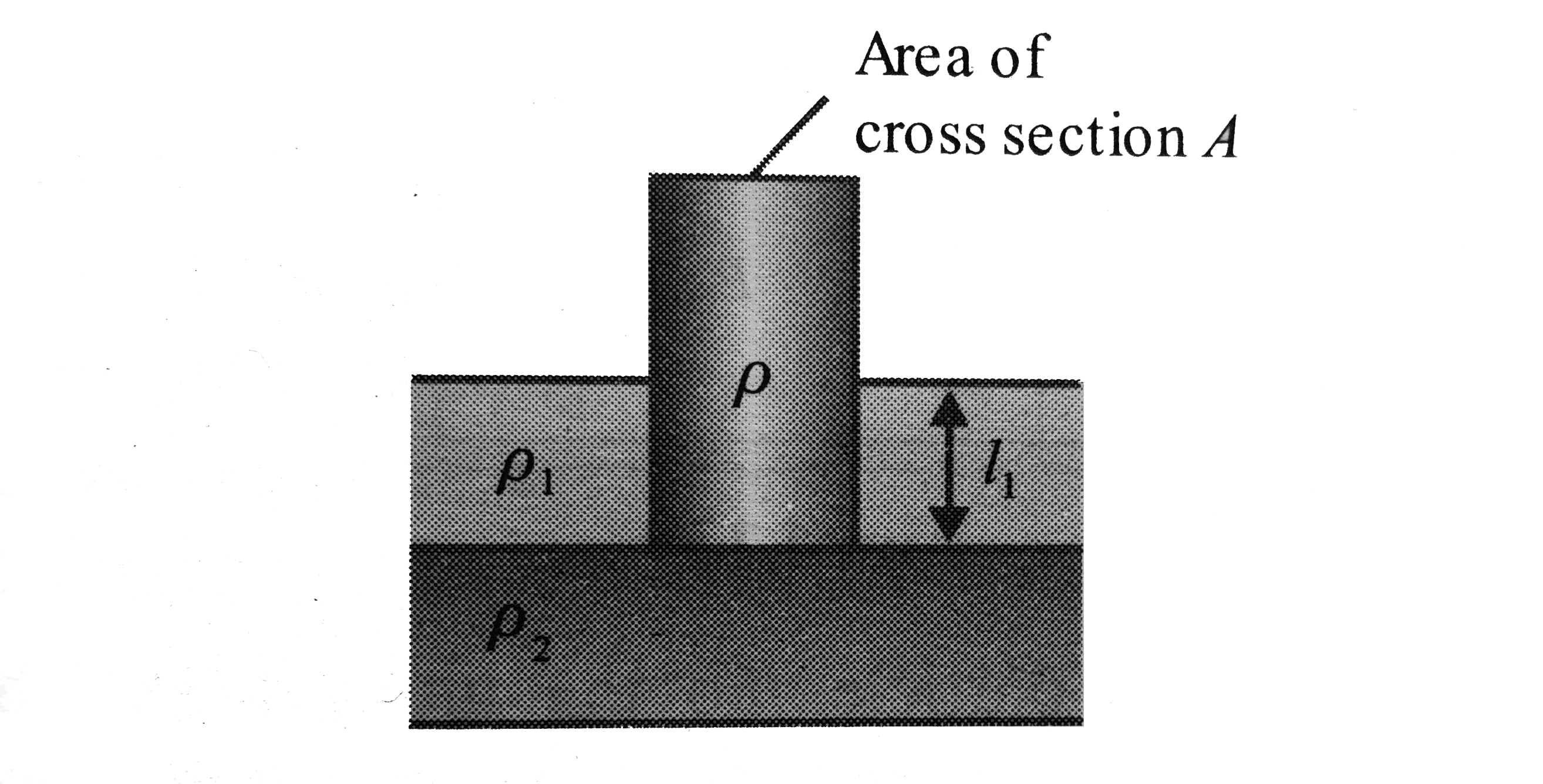
A vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
View Solution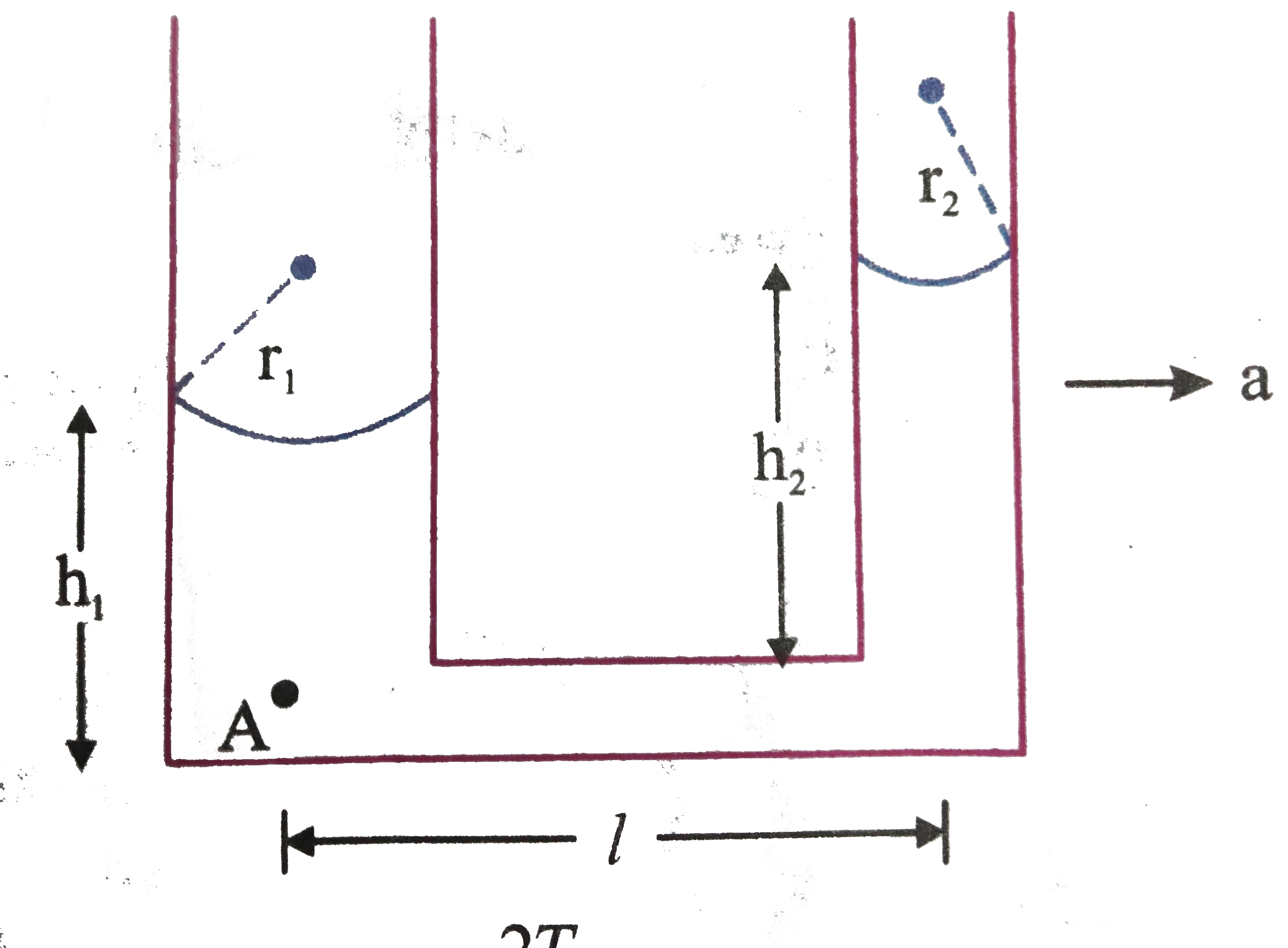
A vertical communicating tube contains a liquid of density ρ. If it moves with a horizontal acceleration a, pressure at A is equal to :
View Solution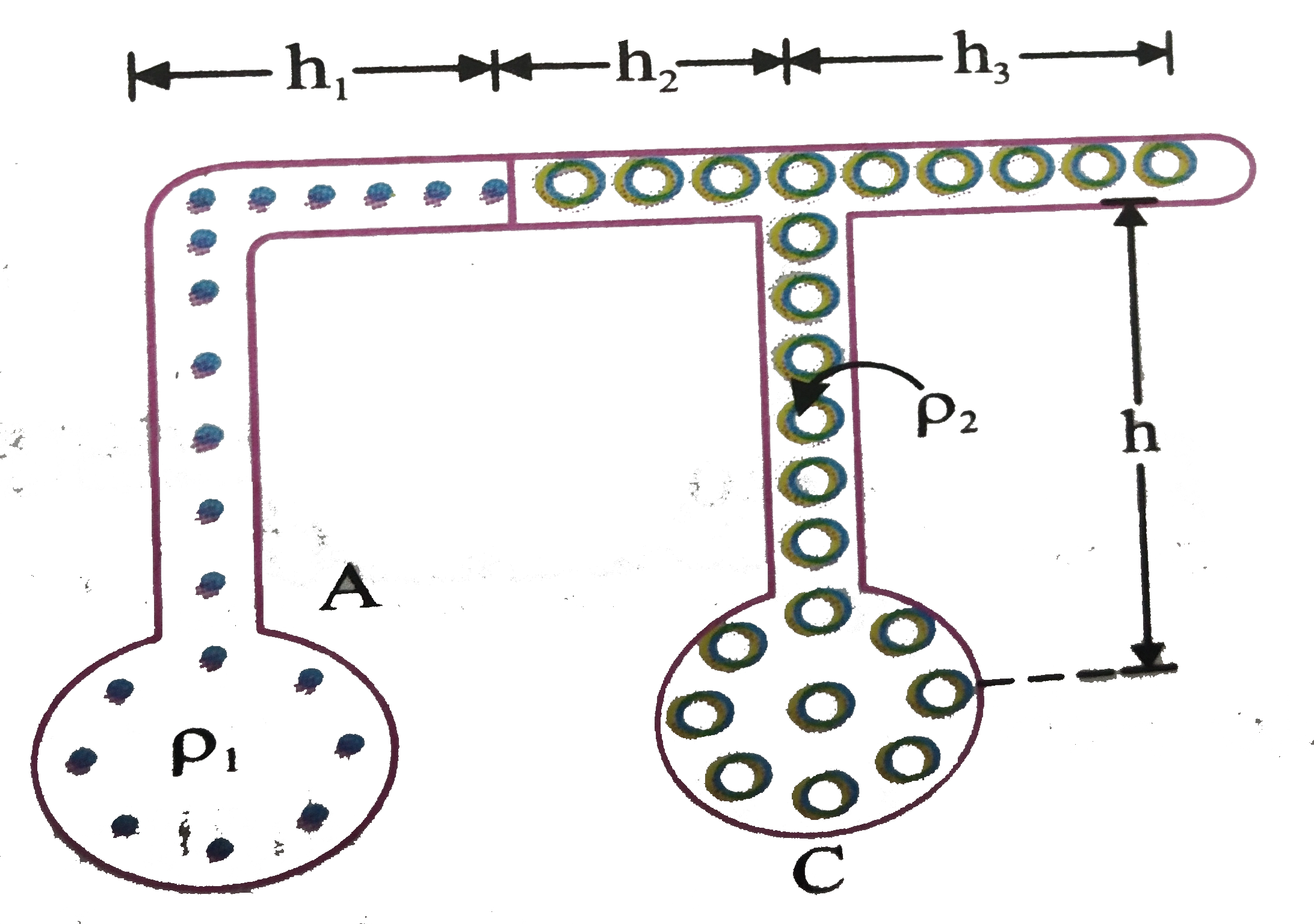
The difference in pressures in bulbs A and C having fluids of densities ρ1 and ρ2 when tube B is horizontal will be
View SolutionIf two liquids of same masses but densities ρ1andρ2 respectively are mixed, then the density of mixture is given by
View SolutionIf two liquids of same masses but densities ρ1andρ2, respectively are mixed, then the density of mixture is given by
View Solution
