Oil enters the bend of a pipe in the horizontal plane with velocity 4ms−1 and pressure 280×103Nm−2 as shown in the figure. Find the pressure of oil at the point Q in (kNm2)
(Take specific gravity of oil as 0.9 and sin37∘=0.6.)

The correct Answer is:172(kNm−2)
Let A1 and A2 be the cross sectional areas of the pipe at points P and Q, respectively.
Let v1 and v2 be velocities of oil at the points P and Q, respectively. By conservation of mass.
Q=A1v1=A2v2⇒v2=(A1A2)(v1)=4v1
Applying Bernoulli's equation between points P and Q we have
P1+12ρv21=P2+12ρv22
P2=P1+12ρ(v21−v22)
=P1+12×0.9[16−256]×103
=280×103+(−108)×103
P2=172×103Nm−2
P2=172(kNm−2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.410videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
The volume of a gas at pressure 1.2×107Nm−2 and temperature 127∘C is 2.0 litre. Find the number of molecules in the gas.
View Solutionwater enters at one end of a horizontal pipe of non-unifrom cross -section with a velocity of 0.4ms−1 and leaves the other end with a velocity of 0.6ms−1 The pressure of water at the first end is 1500Nm−2 Calculate the pressure at the other end Density of water =1000kgm−3
View Solution
Knowledge Check
- Question 1 - Select One
Two horizontal pipes of radii 1 cm and 2cm are connected with one-another. Water is flowing through them. If the velocity of water in first pipe is 8ms−1 and the pressure is 1.0×105Nm−2, then pressure (in N m−2) and velocity (in ms−1) of water in second pipe are (Density of water =103kgm−3)
A1.0×105,8B2×105,16C1.3×105,2D1.8×105,4 - Question 2 - Select One
The velocity of kerosene oil in a horizontal pipe is 5m/s. If g=10m/s2 then the velocity head of oil wlill be
A1.25 mB12.5 mC0.125mD125m - Question 3 - Select One
At a point P in a water pipe line the velocity is 1ms−1 and the pressure is 3×105pa. At another point Q the area of cross section is half that of at P and the pressure is 5×105 pa. The difference of heights between P and Q in metre is (g=10ms−2)
A10.5B20.15C4.5Dzero
Consider a horizontal water pipe connected to a pressure meter. When the pipe is closed the pressure displayed is 4.5×105Nm−2 and when the pipe is openekd the pressure displayed is 4×105Nm−2. Then what is the speed of the water (in standard units) flowing in the pipe ?
View SolutionTwo point charge q1=−10×10−6C and q2=15×10−6 are 40 cm apart as shown in figure. Find the potential difference between the point P and Q.
 View Solution
View SolutionA cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 nd that of ice is 0.9.
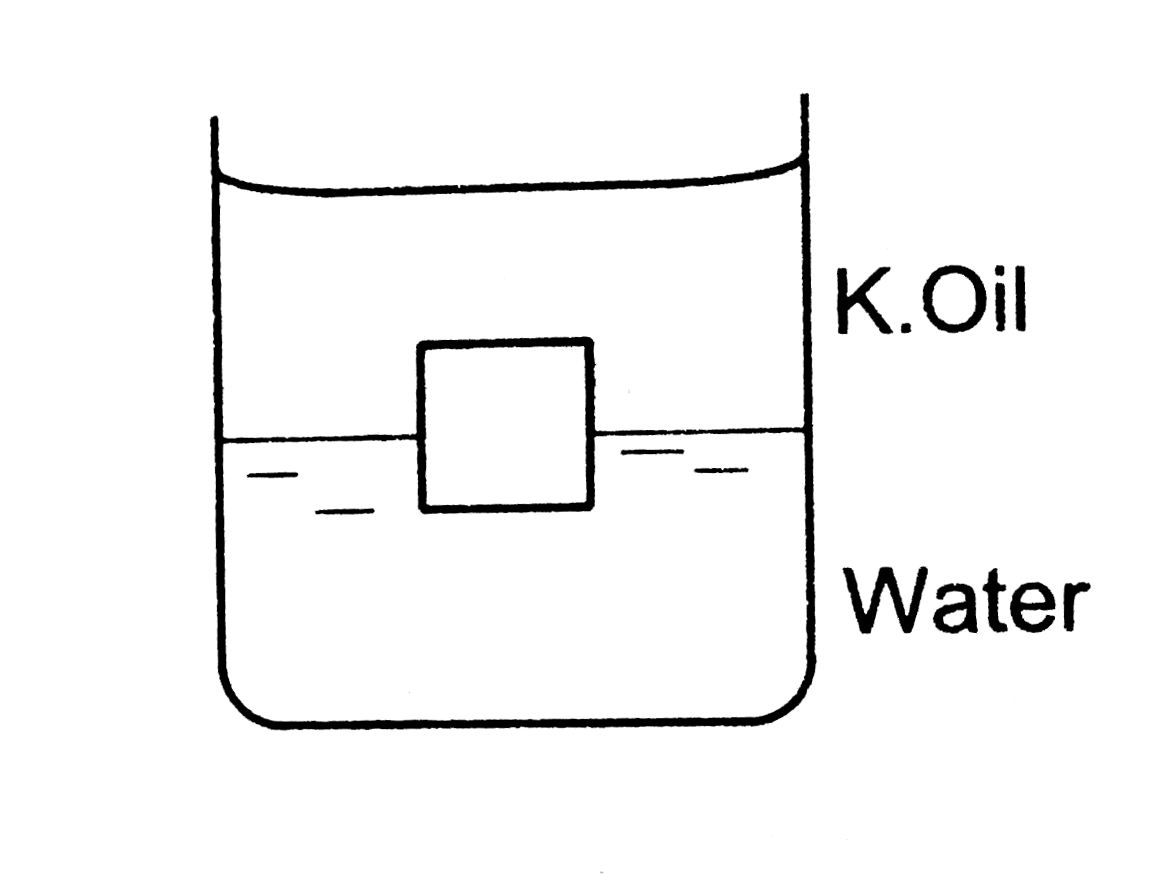 View Solution
View SolutionThe reading of pressure meter attached with a closed pipe is 3.5×105Nm−2. On opening the value of the pipe, the reading of the pressure meter is reduced to 3.0×105Nm−2. Calculate the speed of the water flowing in the pipe.
View SolutionThe density of carbon dioxide gas at 0∘C and at pressure 1.0×105Nm−2is1.98kgm−3. Find the rms velocity of its molecules at 0∘C and also at 30∘C, assuming pressure to be constant.
View Solution

