A resistance R carries a current i. The power lost to the surrounding is λ(θ−θ0). Here, λ is a constant, θ is temperature of the resistance and θ0 is the temperature of the atmosphere. If the corfficient of linear expansion is α. The strain in the resistance is
αλl2R
αλ/R
αl2R2λ
proporitonal to the length of the resistance wire
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the temperature of the body θ and time of cooling 't' and room temperature of the surrounding θ0. The cooling curve is
A B
B C
C D
D
The radius of a ring is R and its coefficient of linear expansion is α. If the temperature of ring increases by θ then its circumfrence will increase by
AπRαθB2πRαθCπRαθ2DπRαθ4The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
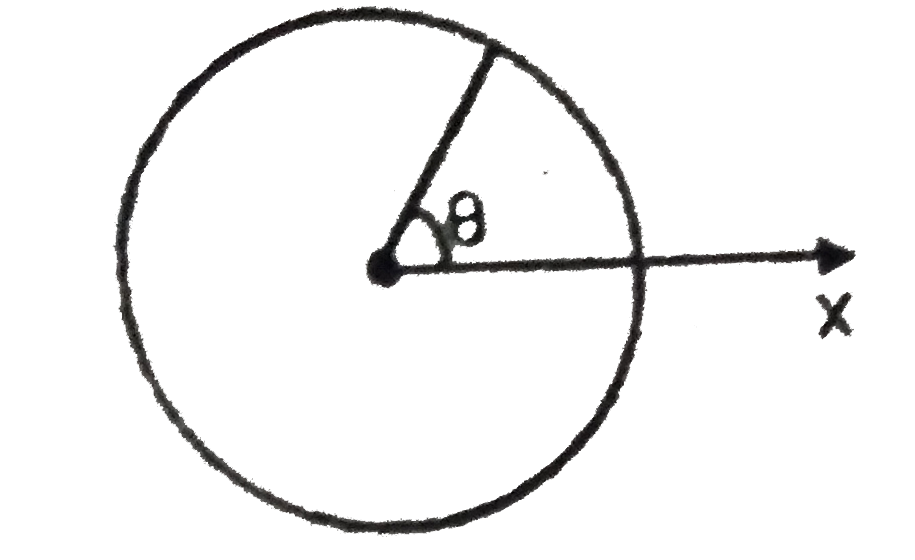 A0Bλ0∈0Cλ0π∈0Dλ02π∈0
A0Bλ0∈0Cλ0π∈0Dλ02π∈0
The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is

View SolutionA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionConsider the two insulating sheets with thermal resistance R1 and R2 as shown in figure. The temperature θ is

View SolutionA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionConsider the two insulating sheets with thermal resistance R1 and R2 as shown in figure. The temperature θ is

View Solution
