A resistor has a resistance of 176 ohms. How many of these resistors should be connected in parallel so that their combination draws a current of 5 amperes from a 220 volt supply line?
The correct Answer is:4 resistors
To solve the problem, we need to determine how many resistors of 176 ohms each should be connected in parallel to draw a total current of 5 amperes from a 220-volt supply. Here’s the step-by-step solution:
Step 1: Calculate the Equivalent Resistance
We start by using Ohm's Law, which states that V=I×R, where:
- V is the voltage (220 volts),
- I is the current (5 amperes),
- R is the equivalent resistance (RAB).
Rearranging the formula gives us:
RAB=VI=220volts5amperes=44ohms
Step 2: Set Up the Parallel Resistance Formula
When resistors are connected in parallel, the equivalent resistance (RAB) can be calculated using the formula:
1RAB=1R+1R+⋯+1R(n times)
Where R is the resistance of each resistor (176 ohms). This can be simplified to:
1RAB=nR
Where n is the number of resistors.
Step 3: Substitute Known Values
We know:
- RAB=44ohms
- R=176ohms
Substituting these values into the equation gives:
144=n176
Step 4: Solve for n
To find n, we can rearrange the equation:
n=17644
Calculating this gives:
n=4
Conclusion
Thus, 4 resistors of 176 ohms each should be connected in parallel to draw a current of 5 amperes from a 220-volt supply line.
---
We start by using Ohm's Law, which states that V=I×R, where:
- V is the voltage (220 volts),
- I is the current (5 amperes),
- R is the equivalent resistance (RAB).
RAB=VI=220volts5amperes=44ohms
When resistors are connected in parallel, the equivalent resistance (RAB) can be calculated using the formula:
1RAB=1R+1R+⋯+1R(n times)
Where R is the resistance of each resistor (176 ohms). This can be simplified to:
1RAB=nR
Where n is the number of resistors.
We know:
- RAB=44ohms
- R=176ohms
144=n176
To find n, we can rearrange the equation:
n=17644
Calculating this gives:
n=4
Thus, 4 resistors of 176 ohms each should be connected in parallel to draw a current of 5 amperes from a 220-volt supply line.
Topper's Solved these Questions
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Very Short Answer Type Questions
1 Videos
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Short Answer Type Questions
2 Videos
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Sample Problem
1 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - NCERT BOOK
2 Videos
Similar Questions
Knowledge Check
How many resistors of 88 W are connected in parallel to carry 10 A current on a 220 V line?
A8 resistorsB5 resistorsC10 resistorsD4 resistorsThe resistance of a heater coil is 110ohm. A resistance R is connected in parallel with it and the combination is joined in series with a resistance of 11ohm to a 220 volt main line. The heater operates with a power of 110 watt. The value of R in ohm is
A12.22B24.22CNegativeDThat the given values are not correctIf three resistors of resistance 2Ω,4Ω and 5Ω are connected in parallel then the total resistance of the combination will be
A2019ΩB1920ΩC1910ΩD1019Ω
Show how you would connect three resistors, each of resistance 6 ω , so that the combination has a resistance of
4 ω
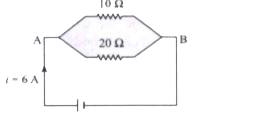
View SolutionTwo resistors of resistance 10Ω and 20Ω are connected in parallel. A battery supplies 6 A of current to the combination. Calculate the current in each resistor.
View SolutionTwo identical resistors of resistance 100±5 ohm are connected parallel. Calculate the eqivalent resistance of the combination.
View SolutionEquivalent resistance R, of the parallel combination when two resistors Rand R, are connected in parallel is equal to
View SolutionThe resistors of resistances 2Ω,4Ω and 8Ω are connected in parallel, then the equivalent resistance of the combination will be
View Solution
