A ring has a total mass M but non-uniformly distributed over its circumference. The radius of the ring is R. A point mass m is placed at the centre of the ring. Workdone in taking away this point mass from ecntre to infinity is
−GMmR
GMmR
−GMm2R
GMmR
The correct Answer is:B
Gravitational potential at the centre of the ring even if mass is non-uniformly distributed on ring
is Vc=−GMR
Gravitational potential at infiity is, Vf=0
Workdone = increase in potential energy
=m(Vf−Vc)=m[0−(−GmR)]=GMmR
Similar Questions
Mass is non - uniformly distributed on the circumference of a ring of radius a and centre at origin . Let b be the distance of centre of mass of the ring from origin. Then ,
View SolutionA charge of 500 μC is distributed uniformly over the circumference of a ring of radius 25 cm. What will be be electric potential at the centre of ring?
View Solution
Knowledge Check
Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2
Find the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
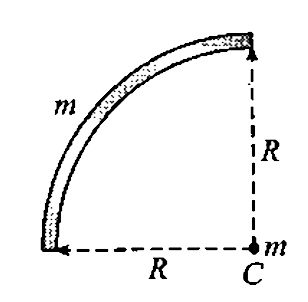
View SolutionA ring of radius R with a uniformly distributed charge q as shown in figure. A charge q0, is now placed at the centre of the ring. Find the increment in-the tension in ring.

View SolutionA ring of radius R has uniformly distributed charge q. A point charge Q is placed at the centre of the ring. (a) Find the increase in tension in the ring after the point charge is placed at its centre. (b) Find the increase in force between the two semicircular parts of the ring after the point charge is placed at the centre. (c) Using the result found in part (b) find the force that the point charge exerts on one half of the ring.
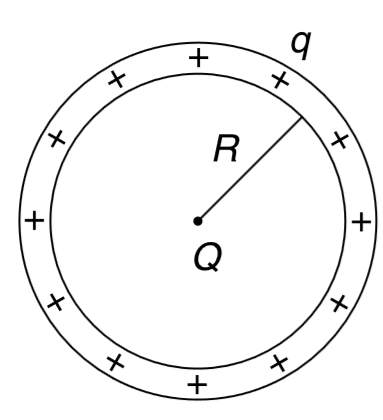
View SolutionA charge +Q is uniformly distributed over a thin ring of a radius R. Find the velocity of a negative point charge -Q at the moment it passes through the centre of the ring if it was initially at rest at infinity on the axis of the ring. The mass of the charge-Q is equal to m.
View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
View SolutionA non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
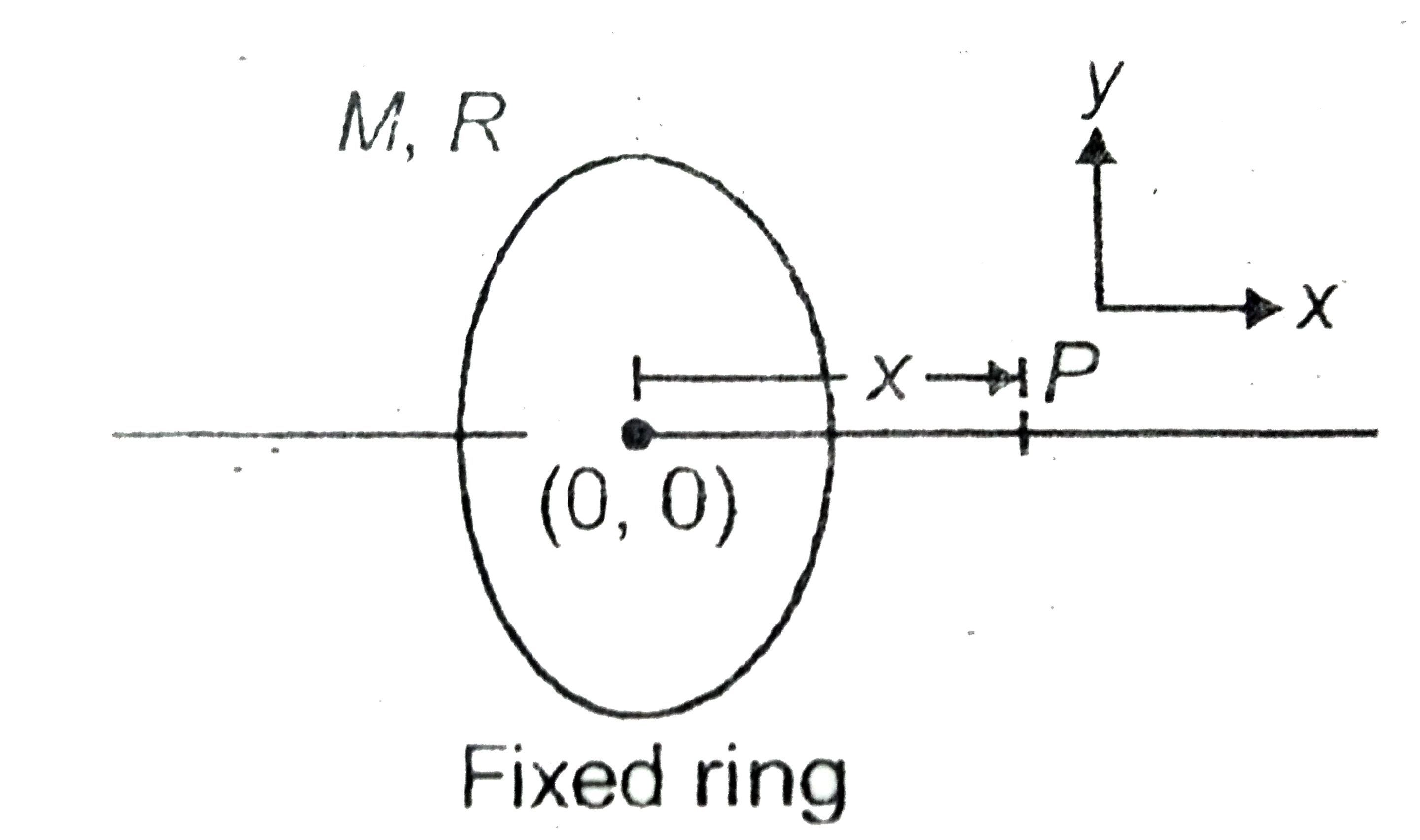
If the point mass m placed at the centre of ring and given a velocity v0 such that point mass escapes from the gravitational field of ring. Then v0 is
View Solution
