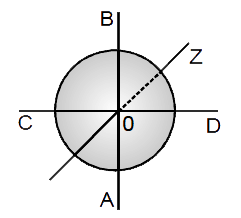
A ring having non-uniform distribution of mass $M$ and radius $R$ is being considered. A point mass $m_{0}$ is taken slowly towards the ring. In doing so, work done by the external force against the gravitational force exerted by ring is

$\frac{G M m_{0}}{\sqrt{2} R}$

$\frac{G M m_{0}}{R} [\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{5}}]$

$\frac{G M m_{0}}{R} [\frac{1}{\sqrt{5}} - \frac{1}{\sqrt{2}}]$

It is not possible to find the required work as the nature of distribution of mass is not known.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

For a uniform ring of mass M and radius R at its centre
Afield and potential both are zero
Bfield is zero but potential is $\frac{G M}{R}$
Cfield is zero but potential is $- G M / R$
Dmagnitude of field is $\frac{G M}{R^{2}}$ and potential $- \frac{G M}{R}$
The total energy of rolling ring of mass m and radius R is
A $3 / 2 m v^{2}$
B $1 / 2 m v^{2}$
C $m v^{2}$
D $5 / 2 m v^{2}$
A ring of mass $m_{1}$ and radius R is fixed in space at some location. An external agent brings a point mass $m_{2}$ from infinity to centre of the ring. Work done by the external agent will be
A $- \frac{G m_{1} m_{2}}{R}$
B $\frac{G m_{1} m_{2}}{R}$
C $\frac{G \sqrt{m_{1}^{2} + m_{2}^{2}}}{R}$
D $\frac{G m_{1} m_{2}}{R (m_{1}^{2} + m_{2}^{2})}$